早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A的坐标为(-6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.(2)过点A作AD⊥x轴,
题目详情
在平面直角坐标系中,点A的坐标为(-6,6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
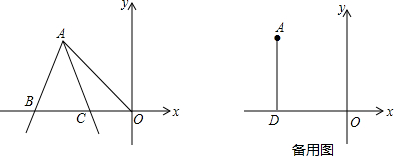
(1)如图1,连接OA,当AB=AC时,试说明:OA=OB.
(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.
▼优质解答
答案和解析
 (1)∵AB=AC,∠BAC=45°,
(1)∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
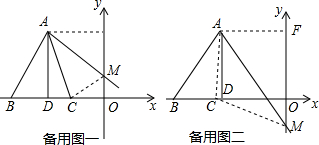
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
,
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
 (1)∵AB=AC,∠BAC=45°,
(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB=67.5°.
过点A作AE⊥OB于E,
则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=
| 1 |
| 2 |
∴∠BAO=67.5°=∠ABC,
∴OA=OB.
(2)设OM=x.
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°,
可知:∠BAD=∠MAF;
∴在△BAD和△MAF中,
|
∴△BAD≌△MAF.
∴BD=FM=6-x.
又∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8-x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即42+x2=(8-x)2,
解得:x=3,
∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,
∴BD=FM=6+x.
同理,
△BAC≌△MAC,
∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:
OC2+OM2=CM2,即82+x2=(4+x)2,
解得:x=6,
∴M点坐标为(0,-6).
看了 在平面直角坐标系中,点A的坐...的网友还看了以下:
用OA绳吊着的电灯因需要移位,用OB绳使之缓缓地向右移动,若OA与OB的夹角从0°缓慢地增至120° 2020-03-31 …
如图,重G的物体通过绳OA、OB拴在半圆支架MN上,开始时,OA与竖直方向成37°角,OB与OA垂 2020-04-07 …
有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重 2020-04-27 …
已知RT△ABC中∠C=90°以AB为斜边构造等腰直角三角形∠AOB=90°OA=OB1是说明OC 2020-05-13 …
向量能比较大小吗?如果OC,OA是平行向量且OC比OA的模大,可以说OC>OA吗?如果不是平行向量 2020-05-16 …
a,b两个是单位向量,a.b=-1/2,且=60度(a,b,c,d都是向量),求c向量模的最大值? 2020-05-16 …
如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.(1)求证AD=AE;(2) 2020-06-27 …
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,点B在⊙O上,BP的延 2020-07-13 …
(2012•泰州)如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB 2020-07-26 …
(2012•泰州)如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB 2020-07-26 …