早教吧作业答案频道 -->数学-->
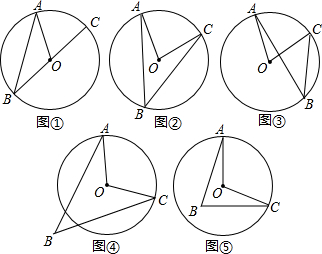
我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③
题目详情
我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.
(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③证明上述结论;
(2)证明上述结论,运用的数学思想方法有:___.
(3)我们把“顶点在圆外的角”称之为“圆外角”,把“顶点在圆内的角”称之为“圆内角”,“圆外角”或“圆内角”是否依然等于“它所对弧上的圆心角度数的一半”?请你分别结合图④、⑤对你的结论加以说明.
(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③证明上述结论;

(2)证明上述结论,运用的数学思想方法有:___.
(3)我们把“顶点在圆外的角”称之为“圆外角”,把“顶点在圆内的角”称之为“圆内角”,“圆外角”或“圆内角”是否依然等于“它所对弧上的圆心角度数的一半”?请你分别结合图④、⑤对你的结论加以说明.
▼优质解答
答案和解析
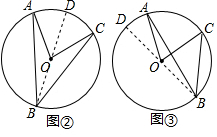 (1)在图①中,∵OA=OB,
(1)在图①中,∵OA=OB,
∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠B=
∠AOC;
在图②中,作直径BD,同①可得∠ABD=
∠AOD,∠CBD=
∠COD,
则∠ABC=
∠AOC;
在图③中,作直径BD.
同理∠CBD=
∠COD,∠ABD=
∠AOD,
∴∠ABC=∠CBD-∠ABD=
∠COD-
∠AOD=
(∠COD-∠AOD)=
∠AOC;
(2)运用了分类讨论思想.
故答案是:分类讨论;
(3)圆外角”或“圆内角”不等于“它所对弧上的圆心角度数的一半”.
如图④.
连接CD.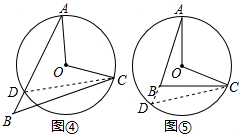
根据(1)可得∠ADC=
∠AOC,
又∵∠ADC>∠B,
∴∠B<
∠AOC;
在图⑤中,延长AB交圆于点D,连接CD.
∵∠D=
∠AOC,
又∵∠D<∠ABC,
∴∠ABC>
∠AOC.
 (1)在图①中,∵OA=OB,
(1)在图①中,∵OA=OB,∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠B=
| 1 |
| 2 |
在图②中,作直径BD,同①可得∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
则∠ABC=
| 1 |
| 2 |
在图③中,作直径BD.
同理∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC=∠CBD-∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)运用了分类讨论思想.
故答案是:分类讨论;
(3)圆外角”或“圆内角”不等于“它所对弧上的圆心角度数的一半”.
如图④.
连接CD.

根据(1)可得∠ADC=
| 1 |
| 2 |
又∵∠ADC>∠B,
∴∠B<
| 1 |
| 2 |
在图⑤中,延长AB交圆于点D,连接CD.
∵∠D=
| 1 |
| 2 |
又∵∠D<∠ABC,
∴∠ABC>
| 1 |
| 2 |
看了 我们知道:圆周角的度数等于它...的网友还看了以下:
3个三角形和3个圆相加得630,4个三角形和3个圆相加等于730.问三角形等于多少?圆3个三角形和 2020-05-17 …
已知三个半径为根号3的圆两两外切,且三角形ABC的每一边都与其中两个圆相切,求三角形ABC的周长. 2020-06-03 …
请你动动脑已知:三角+圆圈=18圆圈+方块=42三角+方块=60三角=()圆圈=()方块=() 2020-06-04 …
圆锥1,圆锥的母线长5,高为3.在它的侧面展开图中,扇形的圆心角是多少度?2,已知某个圆锥的侧面展 2020-07-13 …
我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.(1)请你分”圆周角的一边过圆心“、”圆心 2020-07-29 …
求答两个题…1已知三角形ABC面积为S若利用斜二测画法作三角形ABC的水平放置直观图的面积为3根号 2020-08-01 …
已知AB是圆O的直径.C是圆O上一点,弦CD平分角ACB(1)判断三角形ABD的形状并加以证明(2) 2020-11-03 …
已知3角形3条边的长度,请问如何在CAD里算出角度 2020-12-19 …
一加一等于几?已知两角之比为7:3,它们的差为72度,求这两个角的度数各是多少?圆周率是如何计算导出 2021-01-31 …
1+1=?一加一等于几已知两角之比为7:3,它们的差为72度,求这两个角的度数各是多少?圆周率是如何 2021-01-31 …