已知函数f（x）=lnxx，关于x的不等式f2（x）+af（x）>0只有一个整数解，则实数a的取值范围是（）A.（-ln33，-ln22]B.（-1e，-ln22]C.[ln22，-ln33]D.[ln22，1e）

Question

已知函数f（x）=

(lnx)/(x)，关于x的不等式f²（x）+af（x）>0只有一个整数解，则实数a的取值范围是（　　）

A. （-

(ln3)/(3)，-(ln2)/(2)]

B. （-

(1)/(e)，-(ln2)/(2)]

C. [

(ln2)/(2)，-(ln3)/(3)]

D. [

(ln2)/(2)，(1)/(e)）

Answer 1

（1）f′（x）=(1-lnx)/(x2)，令f′（x）>0，解得：0<x<e，
令f′（x）<0，解得：x>e，
∴f（x）的递增区间为（0，e），递减区间为（e，+∞），故f（x）的最大值是f（e）=(1)/(e)．
x→+∞时，f（x）→0，x→0时，x→-∞，f（1）=0，故在（0，1）时，f（x）<0，在（1，+∞）时，f（x）>0，
函数f（x）的图象如下：

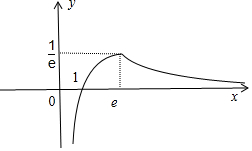
①a<0时，由不等式f²（x）+af（x）>0得f（x）>-a>0或f（x）<0，
而f（x）<0的解集为（0，1）无整数解，f（x）>-a>0的解集整数解一个，
∵f（x）在（0，e）递增，在（e，+∞）递减，
而2<e<3，f（2）=f（4）<f（3），这一个正整数只能为3，
∴f（2）≤-a<f（3），∴-(ln3)/(3)<a≤-(ln2)/(2)
②a=0时，由不等式f²（x）+af（x）>0，得f（x）≠0，解集为（0，1）∪（1，+∞），
整数解有无数多个，不合题意；
③a>0时，由不等式f²（x）+af（x）>0，得f（x）>0或f（x）<-a<0，
∵f（x）<-a<0的解集为（0，1）无整数解，而f（x）>0的解集为（1，+∞），整数解有无数多个，不合题意；
 综上，故选：A