设x1、x2是区间D上的任意两点，若函数y=f(x)满足f(成立则称函数y=f(x)在区间D上下凸.(1)证明函数f(x)=x+在区间(0+∞)上下凸.(2)若函数y=f(x)在区间D上下凸则对任意的x1x2…
成立 则称函数y=f(x)在区间D上下凸. (1)证明函数f(x)=x+ 
在区间(0 +∞)上下凸.
(2)若函数y=f(x)在区间D上下凸 则对任意的x 1 x 2 … x n ∈D 有 
.试根据下凸倒数的这一性质 证明若x 1 x 2 … x n ∈(0 +∞) 则(x 1 +x 2 +…+x n ) 
≥n 2 .
(文)已知S n 是等比数列{a n }的前n项和 且a 3 a 9 a 6 成等差数列 问:S 3 S 9 S 6 是否成等差数列?
答案：(理)证明:(1)设x 1 ＞0 x 2 ＞0 则f( )- ［f(x 1 )+f(x 2 )］
=
= = 
= 
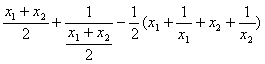
≤0
∴f( )≤ ［f(x 1 )+f(x 2 )］.由定义可知f(x)=x+ 
在区间(0 +∞)上下凸.
(2)由(1)可知f(x)=x+ 在(0 +∞)上下凸
根据性质 有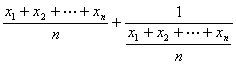 
∴ 
.
∵x 1 x 2 … x n ∈(0 +∞) ∴x 1 +x 2 +…+x n ＞0.
上述可化为(x 1 +x 2 +…+x n ) 
≥n 2 .
(文)由a 3 a 9 a 6 成等差数列，可得a 3 +a 6 =2a 9 即a 1 q 2 +a 1 q 5 =2a 1 q 8 .
∵a 1 q 2 ≠0 ∴1+q 3 =2q 6 .
当q≠1时，S 3 +S 6 = 
=2S 9
∴S 3 S 9 S 6 成等差数列.
当q=1时，S 3 +S 6 =3a 1 +6a 1 =9a 1 而2S 9 =18a 1 .
∵a 1 ≠0 ∴S 3 +S 6 ≠2S 9 .∴S 3 S 9 S 6 不成等差数列.
综合 得当q≠1时，S 3 S 9 S 6 成等差数列，当q=1时，S 3 S 9 S 6 不成等差数列.
1.已知对任意的x∈R,不等式1/2^(x^2+x)>(1/2)^(x^2-mx+m+4)恒成立, 2020-05-21 …
设函数f(x)=(1+x)^2-2ln(1+x)（1）求f(x)的单调区间（2）若当x∈[1/e- 2020-06-18 …
设函数f(x)=(1+x)^2-2ln(1+x).①若当x∈[1/e-1,e-1]时,（其中e=2 2020-06-18 …
麻烦写出完成答案.1.设二维随机变量(X,Y)是有概率密度f(x,y)={ke^[-2x-3y)] 2020-07-22 …
已知二次函数gx=mx∧2-2mx+n+1m＞0在区间0,3(是闭区间)上有最大值4,最小值01求 2020-08-01 …
设函数f(x)=(a/3)x^3-(3/2)x^2+(a+1)x+1,a为实数.1.已知函数f(x 2020-08-03 …
已知函数f(x)=x^2-mlnx,h(x)=x^2-x+a（1）当a=0时,f(x)>=h(x)在 2020-10-31 …
g(x)=ax^2-2ax+1+b,在区间[2,3]上有最大值4,最小值1,设f(x)=g(x)/x 2020-11-04 …
函数着急!已知函数f(x)=axe^x(a不等于0,e为自然对数的底)(1)试着确定函数f(x)的单 2020-11-17 …
已知函数f(x)=x^3/3-mx^2+3mx/2(m>0)（1）若f(x)在区间[1,2]上单调递 2020-12-08 …