如果x0是函数f（x）的一个零点，且在这个零点两侧函数值异号，则称x0是函数f（x）的一个变号零点，已知函数f（x）=ax2+1+lnx在（1e，e）上有且仅有一个变号零点，则实数a的取值范围为（

Question

如果x₀是函数f（x）的一个零点，且在这个零点两侧函数值异号，则称x₀是函数f（x）的一个变号零点，已知函数f（x）=ax²+1+lnx在（

(1)/(e)，e）上有且仅有一个变号零点，则实数a的取值范围为（　　）

A. [-

(2)/(e2)，0）

B. [-

(2)/(e2)，0）∪{-(1)/(2)e}

C. [-

(e)/(2)，0）

D. [-

(2)/(e2)，0]

Answer 1

令f（x）=0得-a=(lnx+1)/(x2)，
令g（x）=(lnx+1)/(x2)，则g′（x）=((1)/(x)•x2-(lnx+1)•2x)/(x4)=(-2lnx-1)/(x3)，
令g′（x）=0得x=e -(1)/(2)，
∴当x∈（(1)/(e)，e -(1)/(2)）时，g′（x）>0，当x∈（e -(1)/(2)，e）时，g′（x）<0，
∴g（x）在（(1)/(e)，e -(1)/(2)）上单调递增，在（e -(1)/(2)，e）上单调递减，
且g（(1)/(e)）=0，g（e）=(2)/(e2)，g（e -(1)/(2)）=(e)/(2)．
作出g（x）的大致函数图象如图所示：

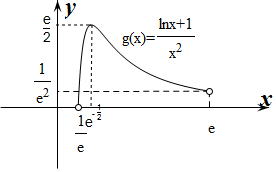
∵f（x）在（(1)/(e)，e）上只有一个零点，∴-a=g（x）在（(1)/(e)，e）上只有1解，
∴0<-a≤(2)/(e2)或-a=(e)/(2)，解得-(2)/(e2)≤a<0或a=-(e)/(2)．
故选B．