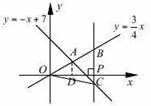
如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的图像交于点A．（1）求点A的坐标；（2）设轴上一点P（，0），过点P

Question

如图，在平面直角坐标系 xOy 中，已知正比例函数 与一次函数 的图像交于点 A ．

（ 1 ）求点 A 的坐标；

（ 2 ）设 轴上一点 P （ ， 0 ），过点 P 作 轴的垂线（垂线位于点 A 的右侧），分别交 和 的图像于点 B 、 C ，连接 OC ，若 BC= OA 求△ OBC 的面积．

Answer 1

1 ） 点 A 的坐标为（ 4 3 ）； （ 2 ）

【解析】

试题分析：（ 1 ） 点 A 是正比例函数 与一次函数 图像的交点坐标，把 _{它们的方程联立组成方程组，方程组的解就是点 A 的横纵坐标；（ 2 ）过点 A 作 x 轴的垂} 线，在 Rt △ OAD 中，由勾股定理求得 OA 的长，再由 BC= OA 求得 OB 的长，用点 P 的横坐标 a 表示出点 B 、 C 的坐标，利用 BC 的长求得 a 值，根据 即可求得 △ OBC 的面积．

试题解析：（ 1 ）由题意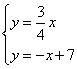得， ，解得 ，

∴ 点 A 的坐标为（ 4 3 ） ．

过点 A 作 x 轴的垂线，垂足为 D ，在 Rt △ OAD 中，由勾股定理得，

∴ ．

∵ P （ a ， 0 ），∴ B （ a ） C （ a -a+7 ），∴ BC= ，

∴ ，解得 a=8 ．

∴ ．

【难度】一般