在平面直角坐标系中，已知平行四边形ABCD的点A（0，-2）、点B（3m，4m+1）（m≠-1），点C（6，2），则对角线BD的最小值是．

Question

在平面直角坐标系中，已知平行四边形ABCD的点A（0，-2）、点B（3m，4m+1）（m≠-1），点C（6，2），则对角线BD的最小值是___．

Answer 1

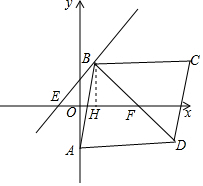如图，∵点B（3m，4m+1），
∴令

3m=x

4m+1=y

，
∴y=(4)/(3)x+1，
∴B在直线y=(4)/(3)x+1上，
∴当BD⊥直线y=(4)/(3)x+1时，BD最小，
过B作BH⊥x轴于H，则BH=4m+1，
∵BE在直线y=(4)/(3)x+1上，且点E在x轴上，
∴E（-(3)/(4)，0），G（0，1）
∵F是AC的中点
∵A（0，-2），点C（6，2），
∴F（3，0）
在Rt△BEF中，
∵BH²=EH•FH，
∴（4m+1）²=（3m+(3)/(4)）（3-3m），
解得：m₁=-(1)/(4)（舍），m₂=(1)/(5)，
∴B（(3)/(5)，(9)/(5)），
∴BD=2BF=2×√((3-(3)/(5))2+((9)/(5))2)=6，
则对角线BD的最小值是6；
故答案为：6．