早教吧作业答案频道 -->数学-->
在正四棱锥S-ABCD中,侧面与底面所成角为,则它的外接球的半径R与内径球半径r的比值为()A.5B.C.10D.
题目详情
在正四棱锥S-ABCD中,侧面与底面所成角为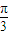 ,则它的外接球的半径R与内径球半径r的比值为( )
,则它的外接球的半径R与内径球半径r的比值为( )
A.5
B.
C.10
D.
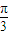 ,则它的外接球的半径R与内径球半径r的比值为( )
,则它的外接球的半径R与内径球半径r的比值为( )A.5
B.

C.10
D.

▼优质解答
答案和解析
【答案】分析:由题意通过侧面与底面所成角为,设出正四棱锥的底面边长,求出斜高,侧棱长,求出内切球的半径与正四棱锥底面边长的关系;利用外接球的球心与正四棱锥的高在同一条直线,结合勾股定理求出,外接球的半径与底面边长的关系,即可得到比值.由于侧面与底面所成角为,可知底面边长与两个对面斜高构成正三角形,设底面边长为a,则斜高也为a,进而可得侧棱长为 ,高为四棱锥的内切球半径就是上述正三角形的内切圆半径为,其外接球球心必在顶点与底面中心连线上,半径为R,球心为O,顶点为P,底面中心为O1,底面一个顶点为B,则OB=OP,于是就有:(-R)2+()2=R2 解得R=.所以两者的比为:.故选D点评:本题是中档题,考查学生的空间想象能力,计算能力推理能力.求出球的半径与正三棱柱的底面边长的关系,是本题的关键.
看了 在正四棱锥S-ABCD中,侧...的网友还看了以下:
关于棱镜常数的问题全站仪使用中,棱镜常数应该设置成多少?棱镜常数一般为多少?棱镜常数有什么简易的测 2020-05-14 …
由某种透明物体制成的等腰直角棱镜ABO,两腰都为16cm,且两腰与Ox和Oy轴都重合,如图所示,从 2020-06-03 …
已知正三棱锥的底面边长为10cm,侧棱与底面所成角为30°.求:(1)三棱锥的高、斜高;(2)侧面 2020-06-04 …
已知三棱锥P-ABC各顶点坐标分别为A(0.0.0)B(2.0.0)C(0.1.0)P(0.0.3 2020-06-06 …
一道几何体表面积填空题已知斜三棱柱直截面(与侧棱垂直且与侧棱都相交的截面)的周长为8,则棱柱的高为 2020-06-27 …
1.正四棱锥的底面边长为a,侧棱和底面成45°角,那么它的侧面积是?2.一个正四棱锥的中截面积是Q 2020-07-30 …
已知斜三棱柱直截面(与侧棱垂直且与侧棱都相交的截面)的周长为8,棱柱的高为4,侧棱与底面成60°角 2020-07-31 …
1.正三棱台ABC-A1B1C1中,A1B1=2a,AB=3a(a>0),侧面和底面所成的二面角为 2020-07-31 …
如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0 2020-07-31 …
已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α 2020-07-31 …