早教吧作业答案频道 -->数学-->
在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.(1)说明△AOB与△CBD全等的理由;(2)求C点坐标;(3)若点E(-3,0),连接EA,在直
题目详情
在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.
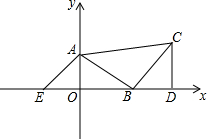
(1)说明△AOB与△CBD全等的理由;
(2)求C点坐标;
(3)若点E(-3,0),连接EA,在直角坐标系中求点P使得△PAE是等腰直角三角形,请直接写出所有符合条件的点P的坐标.

(1)说明△AOB与△CBD全等的理由;
(2)求C点坐标;
(3)若点E(-3,0),连接EA,在直角坐标系中求点P使得△PAE是等腰直角三角形,请直接写出所有符合条件的点P的坐标.
▼优质解答
答案和解析
(1)∵△ABC是等腰直角三角形,∠ABC=90°,CD⊥x轴,
∴∠ABO+∠BAO=90°,∠CBD+∠BCD=90°,∠ABO+∠CBD=90°,AB=BC,
∴∠ABO=∠BCD,∠BAO=∠CBD,
在△AOB与△CBD中,
,
∴△AOB≌△CBD(ASA);
(2)∵△AOB≌△CBD,
∴CD=OB=4,BD=OA=3,
∴点C的坐标为(7,4);
(3)∵点A(0,3),E(-3,0),到原点的距离都为3,
∴要使△APE为等腰直角三角形,点P的坐标为(0,0)或(-3,3)或(0,-3)或(-6,3)或(-3,6)或(3,0).
∴∠ABO+∠BAO=90°,∠CBD+∠BCD=90°,∠ABO+∠CBD=90°,AB=BC,
∴∠ABO=∠BCD,∠BAO=∠CBD,
在△AOB与△CBD中,
|
∴△AOB≌△CBD(ASA);
(2)∵△AOB≌△CBD,
∴CD=OB=4,BD=OA=3,
∴点C的坐标为(7,4);
(3)∵点A(0,3),E(-3,0),到原点的距离都为3,
∴要使△APE为等腰直角三角形,点P的坐标为(0,0)或(-3,3)或(0,-3)或(-6,3)或(-3,6)或(3,0).
看了 在直角坐标系中,△ABC是等...的网友还看了以下:
如图所示四边形ABCD的一组对角∠B,∠D都是直角,求证A,B,C,D四点在同一个圆上 2020-05-13 …
解直角三角形的题目,急在△ABC中,∠C=90度,锐角B满足5sin平方B+sinB-4=0求(1 2020-05-20 …
1:证明四边形AcEF是平行四边形,2:当角B满足什么条伴时,四边形ACEF是菱形,并说理由 2020-06-04 …
如图,在三角形ABC中,角C等于2角B,D是BC上的一点,且AD垂直AB,点E是BD的中点,连接E 2020-06-27 …
在三角形中,A和B满足关系式1/tanAtanB>0,此三角形的形状是A锐角三角形B钝在三角形中, 2020-06-29 …
在ΔABC中,a、b、c分别为三个内角A、B、C的对边,锐角B满足.(1)求的值;(2)若,当ac 2020-07-20 …
在△ABC中,若角A,角B满足关系式1-tanA*tanB 2020-07-21 …
设A,B,C,D是空间内不公面的四点,且满足,则是设A,B,C,D是空间内不公面的四点,且满足向量 2020-07-22 …
如图在四边形ABCD中,角B=∠D=90角a比角c=1比2AB=2CD=1四边形ABCD是一个直角 2020-08-01 …
已知△ABC的内角B满足2cos2B-8cosB+5=0,又若a•b=−9,|a|=3,|b|=5. 2021-02-14 …