如图，在平面直角坐标系中，点A1、A2、A3，…是x轴正半轴上的点，且OA1=A1A2=A2A3=…，分别过点A1、A2、A3，…作y轴的平行线，交反比例函数y=6x（x>0）的图象于点B1、B2、B3，…，则△AnBnBn+1的

Question

如图，在平面直角坐标系中，点A₁、A₂、A₃，…是x轴正半轴上的点，且OA₁=A₁A₂=A₂A₃=…，分别过点A₁、A₂、A₃，…作y轴的平行线，交反比例函数y=

(6)/(x)（x>0）的图象于点B₁、B₂、B₃，…，则△A_nB_nB_n+1的面积等于（　　）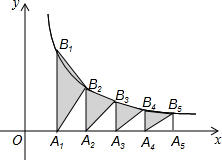

A.

(3)/(n)

B.

(6)/(n)

C.

(3)/(n+1)

D.

(6)/(n+1)

Answer 1

设OA₁=A₁A₂=A₂A₃=…a，
则A₁B₁=(6)/(a)，A₂B₂=(6)/(2a)，A₃B₃=(6)/(3a)，A₄B₄=(6)/(4a)，…，
∴A_nB_n=(6)/(an)，
∴S△AnBnBn+1=(1)/(2)A_nB_n•B_nB_n+1=(3)/(n)．
故选A．