早教吧作业答案频道 -->数学-->
求下列双曲线的实轴长、虚轴长、焦点坐标、顶点坐标、离心率与渐近线方程,并画出图形:(1)x2-8y2=32;(2)y29-x216=1.
题目详情
求下列双曲线的实轴长、虚轴长、焦点坐标、顶点坐标、离心率与渐近线方程,并画出图形:
(1)x2-8y2=32;
(2)
-
=1.
(1)x2-8y2=32;
(2)
| y2 |
| 9 |
| x2 |
| 16 |
▼优质解答
答案和解析
(1)方程可化为
-
=1,∴a=4
,b=2,c=6,
∴实轴长为8
、虚轴长为4、焦点坐标(±6,0)、顶点坐标(±4
,0)、离心率e=
=
,渐近线方程y=±
x;图形如图所示.
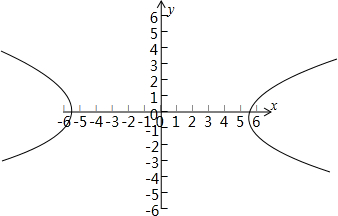
(2)a=3,b=4,c=5,
∴实轴长为6、虚轴长为8、焦点坐标(0,±5)、顶点坐标(0,3)、离心率e=
=
,渐近线方程y=±
x;图形如图所示.
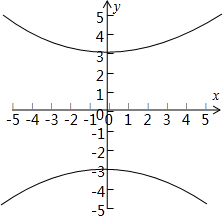
| x2 |
| 32 |
| y2 |
| 4 |
| 2 |
∴实轴长为8
| 2 |
| 2 |
| c |
| a |
3
| ||
| 4 |
| ||
| 4 |
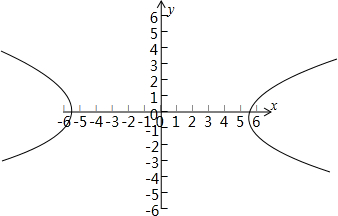
(2)a=3,b=4,c=5,
∴实轴长为6、虚轴长为8、焦点坐标(0,±5)、顶点坐标(0,3)、离心率e=
| c |
| a |
| 5 |
| 3 |
| 4 |
| 3 |
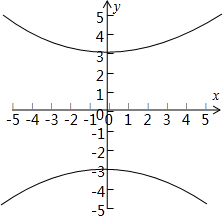
看了 求下列双曲线的实轴长、虚轴长...的网友还看了以下:
脱式计算,能简算的要简算.7.32-(3.8+1.32)95.6×18-9535×8(1-16×3 2020-04-07 …
为测量一座塔的高度,在一座与塔相距20米的楼的楼顶处测得塔顶的仰角为30°,测得塔基的俯角为45° 2020-05-14 …
excel知道平均数和标准差怎么求最大值大体意思是平均值为2.01 标准差为1.32,求在这些数中 2020-05-16 …
(2013•威海)如图,在平面直角坐标系中,直线y=12x+32与直线y=x交于点A,点B在直线y 2020-06-14 …
(2014•沈阳模拟)在平面直角坐标系xOy中,已知椭圆C:x2a2+y2b2=1(a>b>0). 2020-06-21 …
在等比数列{an}中,a3=1/2,a7=1/32,求a5 2020-07-09 …
已知函数f(x)=12(ex+ex-2)(x<1)(其中e是自然对数的底数)的反函数为f-1(x) 2020-08-02 …
阅读下面的文字,回答后面的问题.求3+32+33+…+3100的值.解析令S=3+32+33+…+3 2020-11-07 …
有10个人分蛋糕,分别比例是1:2、1:2、1:4、1:4、1:4、1:4、1:8、1:8、1:16 2020-11-28 …
阅读下列范例,按要求解答问题.例:已知实数a、b、c满足a+b+2c=1,a2+b2+6c+32=0 2020-12-18 …