早教吧作业答案频道 -->数学-->
如图1所示,在边长为1的正方形ABCD中,P是BC边上一动点,AP的延长线与∠ABC的外角平分线交于E,∠EAF=45°,且AF交∠ADC的外角平分线交于F,把△ADF绕A旋转至△ABQ.(Ⅰ)如图1所示,当BE=DF时
题目详情
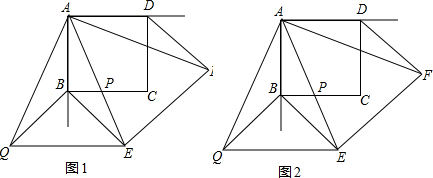
如图1所示,在边长为1的正方形ABCD中,P是BC边上一动点,AP的延长线与∠ABC的外角平分线交于E,∠EAF=45°,且AF交∠ADC的外角平分线交于F,把△ADF绕A旋转至△ABQ.
(Ⅰ)如图1所示,当BE=DF时,求BQ的长;
(Ⅱ)如图2所示.
(1)请探究线段BE,DF,EF之间的数量关系,并证明.
(2)当点P在BC边上运动时,记BP=x(0<x<1),S△BEQ=y,探究y是否随着x的变化而变化,若不变化,求出y的值,若变化,求出y与x的函数关系式.
(Ⅰ)如图1所示,当BE=DF时,求BQ的长;
(Ⅱ)如图2所示.
(1)请探究线段BE,DF,EF之间的数量关系,并证明.
(2)当点P在BC边上运动时,记BP=x(0<x<1),S△BEQ=y,探究y是否随着x的变化而变化,若不变化,求出y的值,若变化,求出y与x的函数关系式.

▼优质解答
答案和解析
(Ⅰ)∵四边形ABCD是正方形,
∴AB=AD=1,∠ABC=∠ADC=∠BAD=90°.
∵BE、DF分别是正方形ABCD的外角平分线,
∴∠EBC=∠CDF=45°.
∴∠ABE=∠ADF=135°.
在△ABE和△ADF中,由于
,
∴△ADF≌△ABE.
∴∠BAE=∠DAF
∵∠EAF=45°,
∴∠DAF=
(90°-45°)=22.5°.
∵∠ADF=135°,
∴∠AFD=22.5°,
∴∠DAF=∠DFA,
∴AB=DF=1.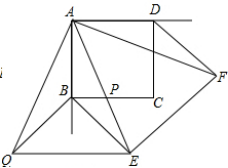
∵△ADF绕A旋转至△ABQ,
∴△ADF≌△ABQ,
∴BQ=DF=1.
(Ⅱ)(1)BE2+DF2=EF2.
证明:∵△ADF≌△ABQ,
∴BQ=DF,AQ=AF,∠QAB=∠DAF=22.5°,∠ADF=∠ABQ=135°,
又∵∠ABE=135°,
∴∠QBE=360°-∠ABQ-∠ABE=90°,
在RT△BQE中,BE2+BQ2=QE2.即BE2+DF2=QE2.
∵∠QAB=∠BAE=∠DAF=22.5°,
∴∠QAE=45°
∴∠QAE=∠EAF.
在△QAE和△FAE中,由于
,
∴△QAE≌△FAE,
∴QE=EF.
∴BE2+DF2=EF2.
(2)当点P在BC边上运动时,
∵∠ADF=∠ABE=135°,
∴∠BAE+∠BEA=45°,
又∵∠DAF+∠BAE=45°,
∴∠DAF=∠AEB.
∴△ABE∽△FDA.
由于△ADF≌△ABQ,
∴△ABE∽△QBA.
∴
=
即BQ×BE=1.
∵△BQE为直角三角形,
∴y=S△QBE=
×BQ×BE=
.
所以y不随x(0<x<1)的变化而变化,恒等于
.
∴AB=AD=1,∠ABC=∠ADC=∠BAD=90°.
∵BE、DF分别是正方形ABCD的外角平分线,
∴∠EBC=∠CDF=45°.
∴∠ABE=∠ADF=135°.
在△ABE和△ADF中,由于
|
∴△ADF≌△ABE.
∴∠BAE=∠DAF
∵∠EAF=45°,
∴∠DAF=
| 1 |
| 2 |
∵∠ADF=135°,
∴∠AFD=22.5°,
∴∠DAF=∠DFA,
∴AB=DF=1.

∵△ADF绕A旋转至△ABQ,
∴△ADF≌△ABQ,
∴BQ=DF=1.
(Ⅱ)(1)BE2+DF2=EF2.
证明:∵△ADF≌△ABQ,
∴BQ=DF,AQ=AF,∠QAB=∠DAF=22.5°,∠ADF=∠ABQ=135°,
又∵∠ABE=135°,
∴∠QBE=360°-∠ABQ-∠ABE=90°,
在RT△BQE中,BE2+BQ2=QE2.即BE2+DF2=QE2.
∵∠QAB=∠BAE=∠DAF=22.5°,
∴∠QAE=45°
∴∠QAE=∠EAF.

在△QAE和△FAE中,由于
|
∴△QAE≌△FAE,
∴QE=EF.
∴BE2+DF2=EF2.
(2)当点P在BC边上运动时,
∵∠ADF=∠ABE=135°,
∴∠BAE+∠BEA=45°,
又∵∠DAF+∠BAE=45°,
∴∠DAF=∠AEB.
∴△ABE∽△FDA.
由于△ADF≌△ABQ,

∴△ABE∽△QBA.
∴
| BQ |
| AB |
| AB |
| BE |
即BQ×BE=1.
∵△BQE为直角三角形,
∴y=S△QBE=
| 1 |
| 2 |
| 1 |
| 2 |
所以y不随x(0<x<1)的变化而变化,恒等于
| 1 |
| 2 |
看了 如图1所示,在边长为1的正方...的网友还看了以下:
数学14455555圆A:(x+2)^2+y^2=1与点A(-2,0),B(2,0),分别说明满足 2020-05-12 …
栓剂的质量要求,不包括()A.塞入腔道后不能融化、软化或溶化B.外形完整光洁C.塞入腔道后无刺激性D 2020-05-31 …
管式泵优点是()简单,成本低,厚壁泵筒承载能力大。A.体积B.外形C.结构D.组成 2020-05-31 …
已知三个半径为根号3的圆两两外切,且三角形ABC的每一边都与其中两个圆相切,求三角形ABC的周长. 2020-06-03 …
铸件设计中,对于壁厚相差悬殊处,采取逐渐过渡圆角连接的主要原因是( )。A.简化工艺B.外形美观C. 2020-06-07 …
起重吊装中,选择设备捆绑点的依据是设备的( )。A.重量B.外形尺寸C.体积D.重心 2020-06-07 …
在边长为a的正三角形A1B1C1内作互相外切且又与...在边长为a的正三角形A1B1C1内作互相外 2020-06-10 …
○A与○B外切,且它们都与○C内切,AB=6,BC=5,AC=4,求三个圆的半径要有过程的 2020-07-14 …
已知m是平面α的一条斜线,点A是平面α外的任意点,是经过点A的一条动直线,那么下列情形中可能出现的 2020-07-30 …
已知某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和六边形两种多边形拼接而成,且有18个顶点 2020-08-01 …