早教吧作业答案频道 -->数学-->
如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
题目详情
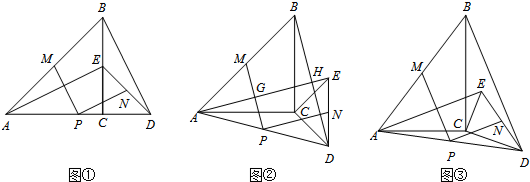
如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

▼优质解答
答案和解析
(1)PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM=
BD,PN=
AE,
∴PM=PM,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN;
(2)∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,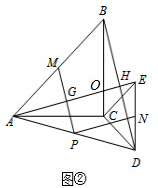
∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=
BD,PM∥BD;
PN=
AE,PN∥AE.
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN.
(3)PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴
=
=k.
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=
BD,PN=
AE.
∴PM=kPN.
(1)PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中
|
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM=
| 1 |
| 2 |
| 1 |
| 2 |
∴PM=PM,
∵PM∥BD,PN∥AE,AE⊥BD,
∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN;
(2)∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,
∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∴△ACE≌△BCD.
∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,

∠CAE=∠CBD,
∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=
| 1 |
| 2 |
PN=
| 1 |
| 2 |
∴PM=PN.
∴∠MGE+∠BHA=180°.
∴∠MGE=90°.
∴∠MPN=90°.
∴PM⊥PN.
(3)PM=kPN
∵△ACB和△ECD是直角三角形,
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD.
∵BC=kAC,CD=kCE,
∴
| BC |
| AC |
| CD |
| CE |
∴△BCD∽△ACE.
∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=
| 1 |
| 2 |
| 1 |
| 2 |
∴PM=kPN.
看了 如图①,△ABC与△CDE是...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
如图,已知平行四边形ABCD,点P在对角线BD上,EF‖BC,GH‖AB,点E,H,F,G分别是在 2020-05-15 …
工人师傅经常利用角尺平分一个任意角.如图所示,∠OB上分别取OD=OEAOB是一个任意角,在边OA 2020-05-17 …
四边形ABCD是由等边△ABC和顶角为120°的等腰△ABD拼成,将一个60°角顶点放在D处,将6 2020-06-18 …
北京师范大学出版社下册184业弟4题的答案工人师傅经常利用角尺平分一个任意角,∠AOB是一个任意角 2020-07-18 …
以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、 2020-07-21 …
以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、 2020-07-21 …
凸四边形公式证明已知凸四边形四边长分别为a,b,c,d,对角线长度分别为e,f,对角线中点的连线长 2020-07-25 …
在△ABC中,角c=90度,AC=6,BC=8,D和E分别是斜边AB和直角边CB上的点,把△ABC 2020-08-02 …
在三角形ABC中,角A角B的平分线分别交对边于D,E角C的外角平分线交对边延长线于F,求证:D、E 2020-08-03 …