早教吧作业答案频道 -->数学-->
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.(1)求AC的解析式;(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;(3)
题目详情
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
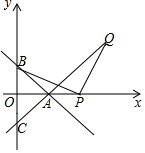
(1)求AC的解析式;
(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;
(3)在(2)的前提下,作PM⊥QC于M,求证:
的值是定值,并求出这一定值.

(1)求AC的解析式;
(2)若在OA的延长线上取一点P,作PQ⊥BP,交直线AC于Q,试探究BP与PQ的数最关系;并证明你的结论;
(3)在(2)的前提下,作PM⊥QC于M,求证:
| MQ-AC |
| PM |
▼优质解答
答案和解析
(1)在y=-x+2中,令y=0可求得x=2,令x=0可求得y=2,
∴A(2,0),B(0,2),
∵OC=OB,
∴点C坐标(0,-2),
设直线AC的解析式为y=kx+b,
把B、C两点坐标代入可得
,解得
,
∴直线AC的解析式为y=x-2;
(2)如图1中,结论:PB=PQ.
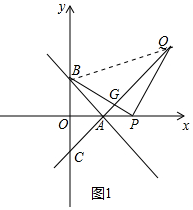
证明如下
:连接BQ,AQ与PB交于点G.
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA=45°,
∴∠CAB=∠BAQ=90°,
∵PB⊥PQ,
∴∠BAG=∠QPG=90°,
∵∠AGB=∠PGQ,
∴△ABG∽△PQG,
∴
=
,
∴
=
,
∵∠BGQ=∠AGP,
∴△BGQ∽△AGP,
∴∠QBG=∠GAP,
∵∠OAC=∠PAG=45°,
∴∠PBQ=∠PAG=45°,
∵∠BPQ=90°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ;
(3)证明:
如图2,作PG⊥PA交PA的延长线于G.
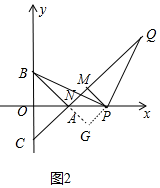
由(2)可知,∠PAM=∠PAG=45°,
∵PM⊥AQ,PG⊥AG,
∴PM=PG,
∵∠G=∠GAM=∠PMA=90°,
∴四边形AMPG是矩形,
∵PM=PG,
∴四边形AMPG是正方形,
∴AG=PM,
在△PMQ和△PGB中,
,
∴△PMQ≌△PGB(AAS),
∴MQ=BG,
∵AB=AC,
∴
=
=
=1.
(1)在y=-x+2中,令y=0可求得x=2,令x=0可求得y=2,
∴A(2,0),B(0,2),
∵OC=OB,
∴点C坐标(0,-2),
设直线AC的解析式为y=kx+b,
把B、C两点坐标代入可得
|
|
∴直线AC的解析式为y=x-2;
(2)如图1中,结论:PB=PQ.

证明如下
:连接BQ,AQ与PB交于点G.
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA=45°,
∴∠CAB=∠BAQ=90°,
∵PB⊥PQ,
∴∠BAG=∠QPG=90°,
∵∠AGB=∠PGQ,
∴△ABG∽△PQG,
∴
| BG |
| GQ |
| AG |
| PG |
∴
| BG |
| AG |
| GQ |
| PG |
∵∠BGQ=∠AGP,
∴△BGQ∽△AGP,
∴∠QBG=∠GAP,
∵∠OAC=∠PAG=45°,
∴∠PBQ=∠PAG=45°,
∵∠BPQ=90°,
∴∠PBQ=∠PQB=45°,
∴PB=PQ;
(3)证明:
如图2,作PG⊥PA交PA的延长线于G.

由(2)可知,∠PAM=∠PAG=45°,
∵PM⊥AQ,PG⊥AG,
∴PM=PG,
∵∠G=∠GAM=∠PMA=90°,
∴四边形AMPG是矩形,
∵PM=PG,
∴四边形AMPG是正方形,
∴AG=PM,
在△PMQ和△PGB中,
|
∴△PMQ≌△PGB(AAS),
∴MQ=BG,
∵AB=AC,
∴
| MQ-AC |
| PM |
| BG-AB |
| PM |
| AG |
| PM |
看了 直线y=-x+2与X轴、y轴...的网友还看了以下:
已知二次函数y=x平方+2xm-m+1求证:不论m为何值,该二次函数图像的顶点p都在函数y=-x平 2020-05-16 …
数论题目(信息安全数学基础),thanksn是合数,p是n的素因数,证明:若p^a整除n,但p^( 2020-05-22 …
已知y+z-x/x+y+z=z+x-y/y+z-x=x+y-z/z+x-y=p,请写出一组符合条件 2020-06-03 …
正整数x,y,p满足方程:x^2+y^2=p(xy-1),求证p=5 2020-06-12 …
如何证明均值定理?均值定理:已知x,y∈R+,x+y=S,x·y=P(1)如果P是定值,那么当且仅 2020-06-16 …
证券问题,要给步骤、伊博森正在考虑投资10000美元于5%收益的国债和一个风险资产组合P,P由两项 2020-07-02 …
概率论数理统计的一道例题,一人进行射击,每次击中的概率为P,射击直至两次为止,以X表示首次击中目标 2020-07-14 …
已知关于x的方程(x-3)(x-2)-p²=0⑴求证:无论p为何值,方程总有两个不相等的实数根;已知 2020-12-23 …
1·直线(a-2)y=(3a-1)x-1,求证无论a取何值时,直线总经过第一象限.2·已知函数f(x 2020-12-23 …
已知圆(x-1)+(y-2)=25直线2ax-y+2a-1=0(1)证无论a取何值时直线l与圆相交( 2020-12-25 …