早教吧作业答案频道 -->数学-->
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;(2)若⊙O半径为1,求菱形ACBP的面积.
题目详情
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
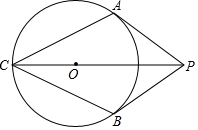
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.

(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
▼优质解答
答案和解析
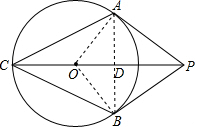 (1)连接AO,BO,
(1)连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=
∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=
OA=
,
∴PD=
,
∴PC=3,AB=
,
∴菱形ACBP的面积=
AB•PC=
.
 (1)连接AO,BO,
(1)连接AO,BO,∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=
| 1 |
| 2 |
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD=
| ||
| 2 |
| ||
| 2 |
∴PD=
| 3 |
| 2 |
∴PC=3,AB=
| 3 |
∴菱形ACBP的面积=
| 1 |
| 2 |
3
| ||
| 2 |
看了 如图,PA、PB是⊙O的切线...的网友还看了以下:
依如图有关基因工程的工具酶功能的叙述,不正确的是()A.切断a处的酶为限制性核酸内切酶B.连接a处 2020-06-05 …
PA,PC是圆的切线,A,C是切点,PBD是割线,与圆交于B,D,求证AC×PA,PC是圆的切线, 2020-07-22 …
圆与直线:题不难,要解题方法过点P(-2,-3)做圆C:(X-4)平方+(Y+2)平方=9的两条切 2020-07-31 …
下图表示限制酶切割某DNA的过程,从图中可知,该限制酶能识别的碱基序列及切点是A.CTTAAG,切 2020-07-31 …
下图表示限制酶切割某DNA的过程,从图中可知,该限制酶能识别的碱基序列及切点是A.CTTAAG,切 2020-07-31 …
(1)如图1,若⊙O1与⊙O2外切于A,BC是⊙O1与⊙O2外公切线,B、C为切点,求证:AB⊥A 2020-07-31 …
(2010•黄浦区二模)以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C,若其中⊙A与⊙B相外切, 2020-07-31 …
如图所示,圆i是R他△ABC的内切圆,角C=90°,圆i和三边分别相切于点D,E,F.如图,圆I是 2020-08-01 …
(2014•沈阳一模)如图,已知圆O1与圆O2外切于点P,直线AB是两圆的外公切线,分别与两圆相切 2020-08-01 …
如图,已知圆O1与圆O2外切于点P,直线AB是两圆的外公切线,分别与两圆相切于A、B两点,AC是圆 2020-08-01 …