早教吧作业答案频道 -->数学-->
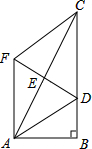
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
题目详情
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
求证:四边形ADCF是菱形.

▼优质解答
答案和解析
证明:∵AF∥CD,
∴∠AFE=∠CDE,
在△AFE和△CDE中,
,
∴△AEF≌△CED.
AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形.
由题意知,AE=AB,∠EAD=∠BAD,AD=AD,
∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
∴∠AFE=∠CDE,
在△AFE和△CDE中,
|
∴△AEF≌△CED.
AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形.
由题意知,AE=AB,∠EAD=∠BAD,AD=AD,
∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
已知正方体ABCD-A1B1C1D1中,E,F分别是C1D1,B1C1的中点,AC交BD=P,A1 2020-05-16 …
设有关系模式R(A,B,C,D,E,F),若有如下的函数依赖集F={A→B,(C,A)→D, (E, 2020-05-24 …
如图,矩形ABCD与圆心在AB上的圆O交于点G,B,F,E,GB=8,AG=1,DE=2,求EF的 2020-07-09 …
我的关于有损分解和无损分解的理解是正确的么?学的有点糊涂,我是这么理解的,假设原来的关系R为(A, 2020-07-12 …
已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H, 2020-07-13 …
数学分析习题.设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b)设函数f(x)在[ 2020-07-16 …
若函数f(x)在R上可导,且f(x)>f'(x),当a>b时,下列不等式成立的是A.e^af(若函 2020-07-29 …
探求凸多面体的面F、顶点数V和棱数E之间的关系得到的结论是()A.无确定关系B.F+E-V=2C. 2020-07-29 …
正方形的6个面分别写着A、B、C、D、E、F,与B、C、E相对的分别是哪个面?F在上面图一上F,前 2020-07-31 …
现在又两块大小相同的直角三角板现有两块大小相同的三角板.三角形ABC,DEF.角ACB=角DFE= 2020-08-02 …