早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.
题目详情
如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两
点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度
为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.
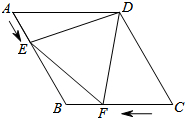
点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度
为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.

▼优质解答
答案和解析
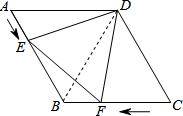 连接BD,
连接BD,
∵在菱形ABCD中,∠ADC=120°,
∴AD=AB,∠A=60°,∠ADB=
∠ADC=60°,
∴△ABD是等边三角形,
∴BD=AD,
∵若△DEF是等边三角形,则∠DEF=60°,DE=DF,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(SAS),
∴AE=BF,
∴当AE=BF时,△DEF是等边三角形,
∵E的速度为1cm/s,点F的速度为2cm/s,
∴AE=tcm,CF=2tcm,
则BF=BC-CF=4-2t(cm),
∴t=4-2t,
解得:t=
.
 连接BD,
连接BD,∵在菱形ABCD中,∠ADC=120°,
∴AD=AB,∠A=60°,∠ADB=
| 1 |
| 2 |
∴△ABD是等边三角形,
∴BD=AD,
∵若△DEF是等边三角形,则∠DEF=60°,DE=DF,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
|
∴△ADE≌△BDF(SAS),
∴AE=BF,
∴当AE=BF时,△DEF是等边三角形,
∵E的速度为1cm/s,点F的速度为2cm/s,
∴AE=tcm,CF=2tcm,
则BF=BC-CF=4-2t(cm),
∴t=4-2t,
解得:t=
| 4 |
| 3 |
看了 如图,在菱形ABCD中,AB...的网友还看了以下:
如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速 2020-04-25 …
如图在四边形ABCD中如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从点D 2020-05-01 …
(2011•石家庄二模)如图1,在梯形ABCD中,AD∥BC,∠C=90°,点E从点B出发,以每秒 2020-05-14 …
如图①,梯形ABCD中,∠C=90°.动点E、F同时从点B出发,点E沿折线BA-AD-DC运动到点 2020-06-12 …
如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动 2020-06-13 …
如图,矩形ABCD中,AB=4cm,AD=3cm,点E从点A出发沿边AB以1cm/s的速度向终点B 2020-06-13 …
设匀强磁场方向沿z轴正向,带负电的运动粒子在磁场中受洛仑兹力f作用的方向沿y轴正向,如图所示,则该 2020-07-02 …
如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度 2020-07-09 …
关于圆的题,要详细过程已知:如图,正方形ABCD中,有一个直径为BC的半圆,BC=2cm,现有两点 2020-07-29 …
如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从点D出发,以每秒1个单位的速 2020-11-01 …