早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.(1)求证:AM=CN;(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.
题目详情
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.
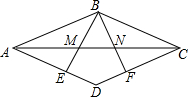
(1)求证:AM=CN;
(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.

(1)求证:AM=CN;
(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.
▼优质解答
答案和解析
(1)证明:如图1中,
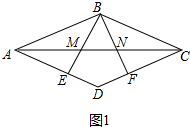
∵四边形ABCD为菱形,
∴AB=BC,∠BAM=∠BCN,∠BAE=∠DAE=∠DCA=∠BCF,
又∵∠AMB=∠CNB=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(ASA),
∴AE=CF.
(2)如图2中,连接BD交AC于O.
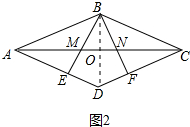
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠BAC=∠DAC,
∵AM=CN(由(1)可知),
∴OM=ON,
∴BD=2OB,AC=2AO,MN=2OM,
∵BD2=MN•AC,
∴4•OB2=2OM•2OA,
∴OB2=OM•OA,
∴
=
,∵∠BOM=∠AOB=90°,
∴△BOM∽△AOB,
∴∠OBM=∠BAO=∠DAC,
∵∠OBM+∠BMO=90°,∠AME=∠OMB,
∴∠EAM+∠AME=90°,
∴∠AEM=90°,即BE⊥AD.

∵四边形ABCD为菱形,
∴AB=BC,∠BAM=∠BCN,∠BAE=∠DAE=∠DCA=∠BCF,
又∵∠AMB=∠CNB=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
|
∴△ABE≌△CBF(ASA),
∴AE=CF.
(2)如图2中,连接BD交AC于O.

∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠BAC=∠DAC,
∵AM=CN(由(1)可知),
∴OM=ON,
∴BD=2OB,AC=2AO,MN=2OM,
∵BD2=MN•AC,
∴4•OB2=2OM•2OA,
∴OB2=OM•OA,
∴
| OB |
| OM |
| OA |
| OB |
∴△BOM∽△AOB,
∴∠OBM=∠BAO=∠DAC,
∵∠OBM+∠BMO=90°,∠AME=∠OMB,
∴∠EAM+∠AME=90°,
∴∠AEM=90°,即BE⊥AD.
看了 如图,在菱形ABCD中,E、...的网友还看了以下:
E是平行四边形ABCD对角线交点,过点A,B,C,D,E分别向直线l引垂线,垂足分别为E是平行四边形 2020-03-31 …
如图,平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别相交于E,F,求证:四边形A如图 2020-05-16 …
正方形ABCD的边长为2,点E在边AD上移动,连接BE,作AP垂直于BE于P,连接CP,点Q在AB 2020-05-17 …
初二平行四边形证明如图所示,已知点AEFD在同一条直线上,AE=DF,BF⊥AD,锤足分别为F、E 2020-05-17 …
在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、 2020-06-15 …
正方形中证明题正方形ABCD中BC边中点E,边接AE.边E做EF垂直AE交正方形ABCD的外角平分 2020-07-13 …
以下说法正确的是()A.在用综合法证明的过程中,每一个分步结论都是结论成立的必要条件B.在用综合法 2020-08-01 …
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了 2020-08-03 …
如图,已知三角形ABC中,AB=AC,AD是BC边上的中点,AE是角BAC的外角平分线,DE平行于 2020-08-03 …
“我们可以得到A和B分别与C、D、E之间的关系”这句话用英语怎么表达“我们可以得到A和B分别与C、D 2020-12-25 …