早教吧作业答案频道 -->数学-->
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.(1)求证:CE=CF;(2)当E为弧CG中点时,求证:BE2=CE•CB.
题目详情
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.
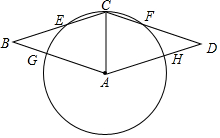
(1)求证:CE=CF;
(2)当E为弧
中点时,求证:BE2=CE•CB.

(1)求证:CE=CF;
(2)当E为弧
 |
| CG |
▼优质解答
答案和解析
(1)证明:连接AE,AF,
∵四边形ABCD是菱形,
∴∠ACB=∠ACF,
∵AE=AC=AF,
∴∠AEC=∠ACE=∠ACF=∠AFC,
∴∠EAC=180°-∠AEC-∠ACE,
∠CAF=180°-∠ACF-∠AFC,
∴∠EAC=∠FAC,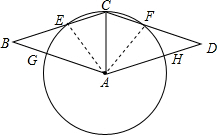
∴
=
,
∴CE=CF;
(2) ∵E为弧
中点,
∴∠CAE=∠BAE,
∵AB=BC,AE=AC,
∴∠ACE=∠AEC=∠BAC=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=AC,
∴△ABC∽△CAE,
∴
=
,
∴AC2=BC•CE,
即BE2=CE•CB.
∵四边形ABCD是菱形,
∴∠ACB=∠ACF,
∵AE=AC=AF,
∴∠AEC=∠ACE=∠ACF=∠AFC,
∴∠EAC=180°-∠AEC-∠ACE,
∠CAF=180°-∠ACF-∠AFC,
∴∠EAC=∠FAC,

∴
 |
| CE |
 |
| CF |
∴CE=CF;
(2) ∵E为弧
 |
| CG |
∴∠CAE=∠BAE,
∵AB=BC,AE=AC,
∴∠ACE=∠AEC=∠BAC=∠B+∠BAE,
∴∠B=∠BAE,
∴BE=AE=AC,
∴△ABC∽△CAE,
∴
| AC |
| BC |
| CE |
| AC |
∴AC2=BC•CE,
即BE2=CE•CB.
看了 如图,菱形ABCD,以A为圆...的网友还看了以下:
弧长及扇形的面积(2)(299:19:53)在矩形ABCD中,AD=2,以点B为圆心,BC为半径画 2020-05-23 …
共有海域经()股东同意可以设定抵押权。A、1/2以上B、2/3以上C、3/4以上D、全体 2020-05-27 …
在不使用增感屏时,n值一般为: ( )A.2以下B.2~3C.4~5D.1以下E.0 2020-06-07 …
对助滤剂添加量的确定,下列表述正确的是A,一般为固体颗粒质量的2%以下B,5%C,0.5%D,1% 2020-07-07 …
已知以点C(a,b)为圆心,半径为r的圆的标准方程为(x-a)2+(y-b)2=r2.例如:以A( 2020-07-16 …
如图,已知在三角形abc中,ab等于4,BC等于2,以点b为圆心,线段bc长为半径的弧交边ac与于 2020-07-22 …
在平面直角坐标系XoY中,已知三点A(-1,0),B(1,0),C(-1,3/2),以A,B为焦点 2020-07-30 …
三角形ABC中,AB=4,BC=2,以点B为圆心,线段BC长为半径的弧交边AC于点D,且角DBC=角 2020-12-25 …
如面各组中,()组的时针和分针所呈现的角一样大.A.1时半和2时半B.8时半和3时半C.10时半和2 2021-01-16 …
下面各组中,()组的时针和分针所呈现的角一样大.A.1时半和2时半B.8时半和3时半C.10时半和2 2021-01-16 …