早教吧作业答案频道 -->数学-->
已知锐角△ABC中,边BC长为12,高AD长为8.(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.①求EFAK的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系
题目详情
已知锐角△ABC中,边BC长为12,高AD长为8.
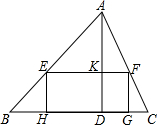
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.

(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求
| EF |
| AK |
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
▼优质解答
答案和解析
(1)①∵EF∥BC,
∴
=
,
∴
=
=
=
,
即
的值是
.
②∵EH=x,
∴KD=EH=x,AK=8-x,
∵
=
,
∴EF=
(8-x),
∴S=EH•EF=
x(8-x)=-
(x-4)2+24,
∴当x=4时,S的最大值是24.
(2)设正方形的边长为a,
①当正方形PQMN的两个顶点在BC边上时,
=
,
解得a=
.
②当正方形PQMN的两个顶点在AB或AC边上时,
∵AB=AC,AD⊥BC,
∴BD=CD=12÷2=6,
∴AB=AC=
=
=10,
∴AB或AC边上的高等于:
AD•BC÷AB
=8×12÷10
=
∴
=
,
解得a=
.
综上,可得
正方形PQMN的边长是
或
.
∴
| AK |
| AD |
| EF |
| BC |
∴
| EF |
| AK |
| BC |
| AD |
| 12 |
| 8 |
| 3 |
| 2 |
即
| EF |
| AK |
| 3 |
| 2 |
②∵EH=x,
∴KD=EH=x,AK=8-x,
∵
| EF |
| AK |
| 3 |
| 2 |
∴EF=
| 3 |
| 2 |
∴S=EH•EF=
| 3 |
| 2 |
| 3 |
| 2 |
∴当x=4时,S的最大值是24.
(2)设正方形的边长为a,
①当正方形PQMN的两个顶点在BC边上时,
| 8-a |
| a |
| 8 |
| 12 |
解得a=
| 24 |
| 5 |
②当正方形PQMN的两个顶点在AB或AC边上时,
∵AB=AC,AD⊥BC,
∴BD=CD=12÷2=6,
∴AB=AC=
| AD2+BD2 |
| 62+82 |
∴AB或AC边上的高等于:
AD•BC÷AB
=8×12÷10
=
| 48 |
| 5 |
∴
| ||
| a |
| ||
| 10 |
解得a=
| 240 |
| 49 |
综上,可得
正方形PQMN的边长是
| 24 |
| 5 |
| 240 |
| 49 |
看了 已知锐角△ABC中,边BC长...的网友还看了以下:
若将数轴折叠,使得A点与-3表示的点重合,则B点与数()表示的点重合若数轴上M、N两点之间的距离为 2020-05-13 …
关于数学平面向量数量积问题..已知:a向量的绝对值=根号2,b向量的绝对值=3,a向量与b向量夹角 2020-05-14 …
一次函数与y轴相交,得锐角,锐角与k的关系.一次函数y=-kx+b(k≠0一次函数与y轴相交,得锐 2020-05-14 …
在一个三角形里,A角的度数是B角度数的4倍,C角的度数是B角度数的5倍,那么你知道A角,B角,C角 2020-06-12 …
在一个三角形里,A角的度数是B角度数的4倍,C角的度数是B角度数的5倍求角的度数分别是?请说明每步 2020-06-12 …
文科数学不考二面角与数列吗 2020-06-27 …
有关数列下列说法正确的是①数列1,2,3与数列3,2,1是同一数列.②数列1,2,3与数列1,2, 2020-07-23 …
根据下面给出的数轴,解答下面的问题:(1)观察数轴,与点A的距离为3的点表示的数是:;(2)若将数 2020-07-30 …
在平面直角坐标系xOy中,一次函数y=kx+b的图象与点A(-3,0),与y轴交于点B,且与正比例函 2020-11-01 …
一个三角形中,角A的度数与角B的度数相加正好与角C度数相等,角A的度数是角C的三分之一,求角B的度数 2020-11-17 …