早教吧作业答案频道 -->数学-->
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D(1)求证:△BFD∽△ABD;(2)求证:DE=DB.
题目详情
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
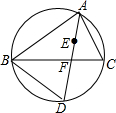
(1)求证:△BFD∽△ABD;
(2)求证:DE=DB.

(1)求证:△BFD∽△ABD;
(2)求证:DE=DB.
▼优质解答
答案和解析
(1)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD.
∵∠BDF=∠ADB,
∴△BFD∽△ABD;
(2)证明:连接BE,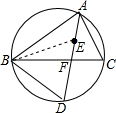
∵点E是△ABC的内心,
∴∠ABE=∠CBE.
又∵∠CBD=∠BAD,
∴∠BAD+∠ABE=∠CBE+∠CBD.
∵∠BAD+∠ABE=∠BED,∠CBE+∠CBD=∠DBE,即∠DBE=∠BED,
∴DE=DB.
∴∠BAD=∠CAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD.
∵∠BDF=∠ADB,
∴△BFD∽△ABD;
(2)证明:连接BE,

∵点E是△ABC的内心,
∴∠ABE=∠CBE.
又∵∠CBD=∠BAD,
∴∠BAD+∠ABE=∠CBE+∠CBD.
∵∠BAD+∠ABE=∠BED,∠CBE+∠CBD=∠DBE,即∠DBE=∠BED,
∴DE=DB.
看了 如图,点E是△ABC的内心,...的网友还看了以下:
初二数学:E(-4,2)F(-1,1),以原点0为位似中心,按比例尺1:2把△EFO缩小,点E的对 2020-05-13 …
如图,圆内接四边形abcd得两边ADDC的延长线相交于点E,DF经过圆心o的圆心,交于AB于点F如 2020-05-17 …
若D是等边三角形ABC的内心,点E,F分别在AC、BC上,且满足CD=3,∠DEF=60°,记△D 2020-07-22 …
O,H分别是三角形ABC的外心,垂心,点D在AB上,AD=AH点E在AC上AE=AO,求证:DE= 2020-07-30 …
椭圆的中心为点E(-10),它的一个焦点为F(-30),相应于焦点F的准线方程为x=则这个椭圆的方 2020-07-31 …
正方形AOBC的边长为4,反比例函数y=k/x的图像经过正方形AOBC的重心D点,E为AO边上任如 2020-08-01 …
如图,正方形AOBC的边长为4,反比例函数y=k/x经过正方形的重心D点,E为AO边上任意一点,F 2020-08-01 …
如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称.(1)画出对称中心E,点E的 2020-08-02 …
E(-4,2)F(-1,1),以原点0为位似中心,按比例尺1:2把△EFO缩小,点E的对应点E`的 2020-08-02 …
(2013•南通)如图,用尺规作出∠OBF=∠AOB,作图痕迹MN是()A.以点B为圆心,OD为半径 2020-11-12 …