早教吧作业答案频道 -->数学-->
如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧MN分别交OA、OB于点M,N.(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转70°得OP′.求证:AP=BP′;(2)点T在左半
题目详情
如图,△OAB中,OA=OB=10,∠AOB=70°,以点O为圆心,6为半径的优弧
分别交OA、OB于点M,N.
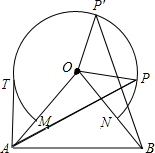
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转70°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
 |
| MN |

(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转70°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与弧相切,求点T到OA的距离;
(3)设点Q在优弧
 |
| MN |
▼优质解答
答案和解析
(1)证明:如图1,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,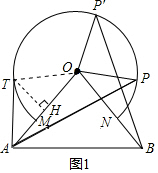
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中
,
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2) 如图1,连接OT,过点T作TH⊥OA于点H,
∵AT是 O的切线,
∴∠ATO=90°,
∴AT=
=
=8,
∵
×OA×TH=
×AT×OT,
即
×10×TH=
×8×6,
解得:TH=
,即点T到OA的距离为
;
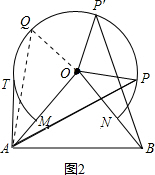
(3) 如图2,当OQ⊥OA时,△AOQ的面积最大;
理由:∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+70°=160°,
当Q点在优弧
右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-70°=20°,
综上所述:当∠BOQ的度数为20°或160°时,△AOQ的面积最大.
∠BOP′=∠POP′+∠BOP=80°+∠BOP,

∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中
|
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2) 如图1,连接OT,过点T作TH⊥OA于点H,
∵AT是 O的切线,
∴∠ATO=90°,
∴AT=
| OA2-OT2 |
| 102-62 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得:TH=
| 24 |
| 5 |
| 24 |
| 5 |

(3) 如图2,当OQ⊥OA时,△AOQ的面积最大;
理由:∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+70°=160°,
当Q点在优弧
 |
| MN |
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-70°=20°,
综上所述:当∠BOQ的度数为20°或160°时,△AOQ的面积最大.
看了 如图,△OAB中,OA=OB...的网友还看了以下:
如图所示,光滑的半球壳半径为R,O点在球心的正下方,一小球乙在距O点很近的A点由静止放开,同时在O 2020-06-14 …
如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA上一 2020-06-17 …
质点从o点起做速度为零的匀加速直线运动,试证明:(1)从o点起在连续相等的时间t内质点所通过的质点 2020-06-26 …
如图所示,O点离地面高度为H,以O点为圆心,制作一四分之一光滑圆弧轨道,小球从与O点等高的圆弧最高 2020-07-31 …
如图,点P是O外一点,PA切O于点A,AB是O的直径,连接OP,过点B作BC∥OP交O于点C,连接 2020-08-01 …
如图,在△ABC中,点O是AC边上的一个动点,过O点作直线MN‖BC,设MN交∠BCA的平分线于点 2020-08-03 …
如图所示,一轻质弹簧固定于O点,另一端系一小球,将小球从与O点在同一水平面且弹簧保持原长的A点无初速 2020-11-01 …
如图,点P是O外一点,PA切O于点A,AB是O的直径,连接OP,过点B作BC∥OP交O于点C,连接A 2020-12-07 …
在任意确定一点O,点P在点O“东偏北60°,3cm"处,点Q在点O"南偏西30°,3cm"处,画出点 2021-01-02 …
记时器的频率是50HZ.O点是地一个点中间还有2个点到A点,O到A点中间断开了,ABCDE是5个连续 2021-01-09 …