早教吧作业答案频道 -->数学-->
如图,O1和O2是外切于点P的两个等圆,点A、B分别在O1、O2上,∠APB=90°,和O1、O2的另一个交点分别是C、D.求证:CD=O1O2.
题目详情
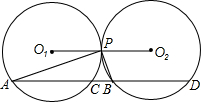
如图, O1和 O2是外切于点P的两个等圆,点A、B分别在 O1、 O2上,∠APB=90°,和 O1、 O2的另一个交点分别是C、D.求证:CD=O1O2.

▼优质解答
答案和解析
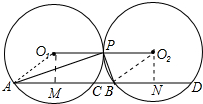
证明:连接O1O2,AO1,BO2,作O1M⊥AD于M,O2N⊥AD于N.
 ∵ O1和 O2外切于点P,
∵ O1和 O2外切于点P,
∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.O1O2∥AB,
∵O1M∥O2N,
∴四边形MNO2O1是平行四边形,
∴O1M=O2N,∵O1M⊥AD,O2N⊥AD,
∴AC=BD(弦心距相等弦相等),
∴AB=CD,
∴CD=2r.
 ∵ O1和 O2外切于点P,
∵ O1和 O2外切于点P,∴接O1O2经过点P,
∵PA⊥PB,
∴∠APB=90°,
∴∠PAB+∠PBA=90°,∠APO1+∠BPO2=90°,
∵O1A=O1P,O2P=O2B,
∴∠O1AP=∠O1PA,∠O2PB=∠O2BP,
∴∠O1AB+∠O2BA=∠O1AP+∠PAB+∠PBA+∠O2BP=180°,
∴AO1∥BO2,∵AO1=BO2,
∴四边形ABO2O1是平行四边形,
∴AB=O1O2=2r.O1O2∥AB,
∵O1M∥O2N,
∴四边形MNO2O1是平行四边形,
∴O1M=O2N,∵O1M⊥AD,O2N⊥AD,
∴AC=BD(弦心距相等弦相等),
∴AB=CD,
∴CD=2r.
看了 如图,O1和O2是外切于点P...的网友还看了以下:
33.14、已知P是抛物线y∧2=2x上的一个动点,过P作圆(x-3) ∧2+y∧2=1的切线,切 2020-05-16 …
已知圆A和圆B的方程分别是(x+2)^2+y^2=25/4,(x-2)^2+y^2=1/4,动圆P 2020-06-09 …
以O为圆心的两个同心圆的半径分别为11cm和9cm,若圆P与这两个圆都相切(1)问符合条件的圆P有 2020-07-08 …
已知点P在以坐标轴为对称轴的椭圆上,点P到两个焦点的距离分别为和,过P作焦点所在轴已知点P在以坐标 2020-07-13 …
(2014•南京三模)在平面直角坐标系xOy中,圆C的方程为(x-1)2+y2=4,P为圆C上一点 2020-07-29 …
在平面直角坐标系中,已知点E(-2,1),连结OE,ABC的三个顶点坐标分别为A(1,4)B(1 2020-07-30 …
以O为圆心的两个同心圆的半径长分别是11cm和9cm,圆P与这两个圆相切(1)问符合条件的圆P有几 2020-08-01 …
急一个圆,圆外任意一点P,过P引圆3条割线与圆相交与6各点,割线分别是(从上倒下)ABCDEF,连A 2020-12-05 …
标题长长长长长长长在一个单位圆中,从圆外一点p做圆的两条切线分别为a,b.p在直线y=x-2上,连接 2021-01-02 …
已知动圆P与圆C1:(x+5)2+y2=49和圆C2:(x-5)2+y2=1,分别求满足下列条件的动 2021-01-11 …