早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.(1)求证:AD平分∠BAC;(2)若⊙O的直径为10,sin∠DAC=55,求BD的长.
题目详情
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
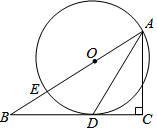
(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=
,求BD的长.

(1)求证:AD平分∠BAC;
(2)若⊙O的直径为10,sin∠DAC=
| ||
| 5 |
▼优质解答
答案和解析
(1)连接OD.
∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)如图2所示:连接ED.
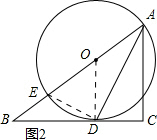
∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC=
,
∴AD=
×10=4
.
∴DC=
×4
=4,AC=
×4
=8.
∵OD∥AC,
∴△BOD∽△BAC,
∴
=
,即
=
,
解得:BD=
.
∵OD、OA是⊙O的半径,
∴OA=OD.
∴∠OAD=∠ODA.
∵点D是⊙O的切点,
∴∠ODC=90°
又∵∠C=90°,
∴OD∥AC.
∴∠ODA=∠DAC,
∴∠OAD=∠CAD,
∴AD平分∠BAC.
(2)如图2所示:连接ED.

∵⊙O的半径为5,AE是圆O的直径,
∴AE=10,∠EDA=90°.
∵∠EAD=∠CAD,sin∠DAC=
| ||
| 5 |
∴AD=
2
| ||
| 5 |
| 5 |
∴DC=
| ||
| 5 |
| 5 |
2
| ||
| 5 |
| 5 |
∵OD∥AC,
∴△BOD∽△BAC,
∴
| OD |
| AC |
| BD |
| BC |
| 5 |
| 8 |
| BD |
| BD+4 |
解得:BD=
| 20 |
| 3 |
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
1.PT切圆O于T,CT为直径,D为OC上的一点,支线PD交圆O于B和A,B在线段PD上,若CD= 2020-04-12 …
三角函数,SOS!如图,在花园小区内有一超市O,已知:文化活动中心A在超市O北偏东30°的方向,物 2020-04-27 …
已知⊙O的半径为4cm,A为线段OP的中点,当OP=7cm时,点A与⊙O的位置关系是()A.点A在 2020-04-27 …
两只小环O和O′分别套在静止不动的竖直杆AB和A′B′上.一根不可伸长的绳子,一端系在A′点上,绳 2020-05-13 …
如图所示,一个均匀的带电圆环,带电荷量为+Q,半径为R,放在绝缘水平桌面上.圆心为O点,过O点作一 2020-05-13 …
已知,cd是⊙o的玄,a为弧cd的中点,e为cd延长线上一点,eg切⊙o于g,ag交cd于k 2020-05-16 …
将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.如图,将矩形变为 2020-05-16 …
一道化学题!关于求相对分子质量的在A+B=C+2D的反应中,一直2.9gA跟4.9gB完全反应生成 2020-05-16 …
(2014•崇明县二模)在⊙O中,圆心O在坐标原点上,半径为210,点P的坐标为(4,个),那么点 2020-05-17 …
读我国某地等高线地形图回答问题图中河流的总体走向是怎样的在A-F六个字母表示的地点中,比较适宜修建 2020-05-17 …