早教吧作业答案频道 -->数学-->
如图所示,直线DP和圆O相切于点C,交直线AE的延长线于点P,过点C作AE的垂线,交AE于点F,交圆O于点B,作平行四边形ABCD,连接BE,DO,CO.(1)求证:DA=DC;(2)求∠P及∠AEB的大小.
题目详情
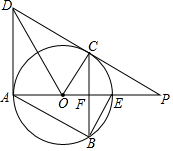
如图所示,直线DP和圆O相切于点C,交直线AE的延长线于点P,过点C作AE的垂线,交AE于点F,交圆O于点B,作平行四边形ABCD,连接BE,DO,CO.
(1)求证:DA=DC;
(2)求∠P及∠AEB的大小.

(1)求证:DA=DC;
(2)求∠P及∠AEB的大小.
▼优质解答
答案和解析
(1)证明:在平行四边形ABCD中,AD∥BC,
∵CB⊥AE,
∴AD⊥AE,
∴∠DAO=90°,
∵DP与⊙O相切于点C,
∴DC⊥OC,
∴∠DCO=90°,
在Rt△DAO和Rt△DCO中,
,
∴Rt△DAO≌△Rt△DCO,
∴DA=DC.
(2)∵CB⊥AE,AE是直径,
∴CF=FB=
BC,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴CF=
AD,
∵CF∥DA,
∴△PCF∽△PDA,
∴
=
=
,
∴PC=
PD,DC=
PD,
∵DA=DC,
∴DA=
PD,
在Rt△DAP中,∠P=30°,
∵DP∥AB,
∴∠FAB=∠P=30°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB=60°.
∵CB⊥AE,
∴AD⊥AE,
∴∠DAO=90°,
∵DP与⊙O相切于点C,
∴DC⊥OC,
∴∠DCO=90°,
在Rt△DAO和Rt△DCO中,
|
∴Rt△DAO≌△Rt△DCO,
∴DA=DC.
(2)∵CB⊥AE,AE是直径,
∴CF=FB=
| 1 |
| 2 |

∵四边形ABCD是平行四边形,
∴AD=BC,
∴CF=
| 1 |
| 2 |
∵CF∥DA,
∴△PCF∽△PDA,
∴
| PC |
| PD |
| CF |
| DA |
| 1 |
| 2 |
∴PC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DA=DC,
∴DA=
| 1 |
| 2 |
在Rt△DAP中,∠P=30°,
∵DP∥AB,
∴∠FAB=∠P=30°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB=60°.
看了 如图所示,直线DP和圆O相切...的网友还看了以下:
关于初三数学拓展(二)的一个问题如图,已知圆心O1和圆心O2相较于点A、B,分别过A、B作直线交O1 2020-03-30 …
1、四边形ABCD是一张矩形纸片,已知AB=15cm,BC=25cm,以对角线BD为折痕,把它折叠 2020-05-16 …
扇形OAB的圆心角为90°,四边形OCDE是边长为1的正方形如图,扇形AOB的圆心角为90°,四边 2020-05-17 …
渠道中线圆曲线主点是指( )。A.直圆点 B.曲中点 C.圆直点 D.转折点 E.圆圆点 2020-05-18 …
已知直线y=-4分之3x+6的图像交x轴与点A,交y轴于点B,在线段OA上找一点E,将△ABE沿着 2020-06-14 …
如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥ 2020-06-23 …
如图,∠ACB=30°,D为CB上一点,CD=3,OD⊥BC于D,交CA于O,以O为圆心,OD为半 2020-07-17 …
在圆O中有一条非直径的弦AB,D是劣弧AB上任意一点,过A、D、B的切线分别相交得点C、E,优弧A 2020-07-20 …
已知AB为圆o直径,点C,D,E是弧ADB上的点,AC=CD=4,DE=BE=4倍根号2,求直径A 2020-07-29 …
如图所示为一列向左传播的横波某时刻的图象,下列说法不正确的是()A.质点c、e的运动方向始终相反B. 2020-12-15 …