早教吧作业答案频道 -->数学-->
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.(1)求证:PO平分∠APC;(2)连接DB,若∠C=30°,求证:DB∥AC.
题目详情
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
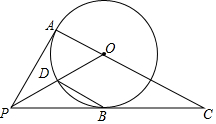
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.

(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
▼优质解答
答案和解析
(1)如图,连接OB,
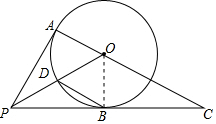
∵PA,PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,
∴PO平分∠APC;
(2)∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°-∠C=90°-30°=60°,
∵PO平分∠APC,
∴∠OPC=
∠APC=
×60°=30°,
∴∠POB=90°-∠OPC=90°-30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP-∠OBD=90°-60°=30°,
∴∠DBP=∠C,
∴DB∥AC.

∵PA,PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,
∴PO平分∠APC;
(2)∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°-∠C=90°-30°=60°,
∵PO平分∠APC,
∴∠OPC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠POB=90°-∠OPC=90°-30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP-∠OBD=90°-60°=30°,
∴∠DBP=∠C,
∴DB∥AC.
看了 如图,PA,PB是⊙O的切线...的网友还看了以下:
已知点P是矩形ABCD外一点,PA⊥面ABCD,且PB,PD与平面ABCD所成角分别为45°,30 2020-05-16 …
如图,E点为x轴正半轴上一点,⊙E交x轴于A、B两点,交y轴于C、D两点,P点为劣弧BC上一个动点 2020-06-12 …
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=3,BC=1,PA 2020-07-06 …
如图,点E为x轴正半轴上一点,E交x轴于A、B两点,交y轴于C、D两点,P点为劣弧BC上一个动点, 2020-07-18 …
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=.(Ⅰ)求点 2020-07-20 …
已知平面α内有一个以AB为直径的圆,PA⊥α,点C在圆周上(不同于A、B两点),点D、E分别是点A 2020-07-30 …
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=3,PA⊥面ABCD 2020-07-31 …
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,.(Ⅰ)求点C到平 2020-07-31 …
在平面直角坐标系中,点B的坐标为(2,0),过点B作AB⊥x轴,交y=mx(m>0)的图象于点A, 2020-08-01 …
立体几何问题在四棱锥P—ABCD中,底面ABCD是直角梯形,其中AB//CD,∠ABC=90°,且 2020-08-02 …