早教吧作业答案频道 -->数学-->
如图,AB是O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交O于点D,连接CD并延长交AB的延长线于点F.(1)求证:CF是O的切线;(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根
题目详情
如图,AB是 O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交 O于点D,连接CD并延长交AB的延长线于点F.
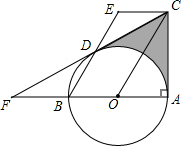
(1)求证:CF是 O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)

(1)求证:CF是 O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
▼优质解答
答案和解析
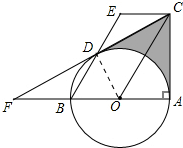
(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,
∴OC∥BE,
∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DOC=∠AOC,
在△COD和△COA中,
,
∴△COD≌△COA,
∴∠CAO=∠CDO=90°,
∴CF⊥OD,
∴CF是 O的切线.
(2) ∵∠F=30°,∠ODF=90°,
∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠DBO=60°,
∵∠DBO=∠F+∠FDB,
∴∠FDB=∠EDC=30°,
∵EC∥OB,
∴∠E=180°-∠OBD=120°,
∴∠ECD=180°-∠E-∠EDC=30°,
∴EC=ED=BO=DB,
∵EB=4,
∴OB=OD═OA=2,
在RT△AOC中,∵∠OAC=90°,OA=2,∠AOC=60°,
∴AC=OA•tan60°=2
,
∴S阴=2•S△AOC-S扇形OAD=2×
×2×2
-
=4
-
.
∵四边形OBEC是平行四边形,
∴OC∥BE,
∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DOC=∠AOC,
在△COD和△COA中,
|

∴△COD≌△COA,
∴∠CAO=∠CDO=90°,
∴CF⊥OD,
∴CF是 O的切线.
(2) ∵∠F=30°,∠ODF=90°,
∴∠DOF=∠AOC=∠COD=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴∠DBO=60°,
∵∠DBO=∠F+∠FDB,
∴∠FDB=∠EDC=30°,
∵EC∥OB,
∴∠E=180°-∠OBD=120°,
∴∠ECD=180°-∠E-∠EDC=30°,
∴EC=ED=BO=DB,
∵EB=4,
∴OB=OD═OA=2,
在RT△AOC中,∵∠OAC=90°,OA=2,∠AOC=60°,
∴AC=OA•tan60°=2
| 3 |
∴S阴=2•S△AOC-S扇形OAD=2×
| 1 |
| 2 |
| 3 |
| 120π•22 |
| 360 |
| 3 |
| 4π |
| 3 |
看了 如图,AB是O的直径,∠BA...的网友还看了以下:
下列关于赤道的叙述,正确的是()A.最长的经线B.最长的纬线C.东西半球的划分界线D.东西经的分界 2020-04-23 …
下列有关赤道的说法,正确的是()A.最长的纬线和南北半球分界线B.最长的纬线和东西半球分界线C.最 2020-04-24 …
神经纤维的构成是()A.胞体、轴突、树突B.长的树突和胞体C.树突和轴突D.轴突、长的树突和髓鞘 2020-05-13 …
神经纤维指的是()A、轴突B、长的树突C、长的树突和轴突D、轴突或长的树突以及套在外面的髓鞘 2020-05-13 …
神经纤维是指神经细胞的()A.较短的突起B.较长的突起C.较短的突起和较长的突起D.轴突或长的树突 2020-05-13 …
在平行六面体ABCD-A'B'C'D'中,向量、、、是A有相同起点的向量B等长的向量C共面向量D不 2020-05-13 …
若a/b=b/c=c/d=d/a,则(a-b+c-d)/(a+b+d-c)的值为 2020-05-13 …
将一细铅丝圆圈剪成A、B、C三段弧,A弧长是B弧长的1/3,B弧长是C弧长的1/2,则最长的弧所对 2020-05-21 …
有关于几个初一地理问题.1.下列关于本初子午线的说法正确的是;A.东西半球的分界线B.最长的经线C 2020-05-22 …
活扳手、管钳的规格是以其( )尺寸来代表的。A.全长B.全长的一半C.使用D.标称 2020-05-30 …