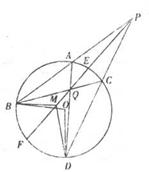
如图过圆O外一点P作该圆的两条割线PAB和PCD分别交圆O于点ABCD弦AD和BC交于Q点，割线PEF经过Q点交圆O于点E、F，点M在EF上，且:(I)求证:PA·PB=PM·PQ.(II)求证：.

Question

如图 过圆O外一点P作该圆的两条割线PAB和PCD 分别交圆 O于点A B C D弦AD和BC交于Q点，割线PEF经过Q点交圆 O于点E、F，点M在EF上，且 :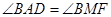

(I)求证:PA·PB=PM·PQ.

(II)求证： .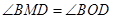

 

 

Answer 1

(I) 见解析；(II) 见解析.

分 析：
(I)证明A Q M B四点共圆，可得结论； (II)先证明，再证明，可得，，所以. 试题
解析：
（Ⅰ）∵∠BAD＝∠BMF，所以A Q M B四点共圆，     3分 所以.      5分 (Ⅱ)∵    ∴  ， 又      所以，     7分 ∴  则       8分 ∵，∴ 所以.       10分
考点：
1、几何证明.