早教吧作业答案频道 -->数学-->
在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).(1)当b=1时,求抛物线相应的函数表达式;(2)当b=1时,如图,E(t,0)是线段BC上
题目详情
在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
(1)当b=1时,求抛物线相应的函数表达式;
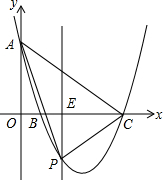
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.

(1)当b=1时,求抛物线相应的函数表达式;
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
▼优质解答
答案和解析
(1)当b=1时,将点B(1,0)代入抛物线y=x2-6mx+5中,得m=1,
∴y=x2-6x+5;
(2)如图1中,直线AC与PE交于点F.
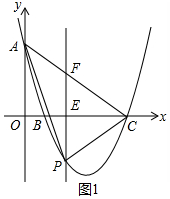
当b=1时,求得A(0,5),B(1,0),C(5,0),可得AC所在的一次函数表达式为y=-x+5,
∵E(t,0),
∴P (t,t2-6t+5),直线l与AC的交点为F(t,-t+5),
∴PF=(-t+5)-(t2-6t+5)=-t2+5t,
∴S△APC=
×(-t2+5t)•5=-
(t-
)2+
,
∵-
<0,
∴当t=
时,面积S有最大值
;
(3)①当b整数时,n为整数,
∴n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中,
得b2-mb+5=0 ①,(b+4)2-m(b+4)+5=0 ②,
由①②可得b2+4b-5=0,解得b=1或-5(舍);
或由一元二次方程根与系数的关系得 b(b+4)=5解得b=1或-5(舍).
②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-mx+5=0的两个根,同样可得b=
或
(舍弃);
∴b=1或
.
∴y=x2-6x+5;
(2)如图1中,直线AC与PE交于点F.

当b=1时,求得A(0,5),B(1,0),C(5,0),可得AC所在的一次函数表达式为y=-x+5,
∵E(t,0),
∴P (t,t2-6t+5),直线l与AC的交点为F(t,-t+5),
∴PF=(-t+5)-(t2-6t+5)=-t2+5t,
∴S△APC=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 125 |
| 8 |
∵-
| 5 |
| 2 |
∴当t=
| 5 |
| 2 |
| 125 |
| 8 |
(3)①当b整数时,n为整数,
∴n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中,
得b2-mb+5=0 ①,(b+4)2-m(b+4)+5=0 ②,
由①②可得b2+4b-5=0,解得b=1或-5(舍);
或由一元二次方程根与系数的关系得 b(b+4)=5解得b=1或-5(舍).
②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-mx+5=0的两个根,同样可得b=
-5+3
| ||
| 2 |
-5-3
| ||
| 2 |
∴b=1或
-5+3
| ||
| 2 |
看了 在平面直角坐标系中,抛物线y...的网友还看了以下:
如图,在平面直角坐标系xoy中,已知抛物线的对称轴为y轴,经过(0,1),(-4,5)两点, 2020-05-16 …
如图所示,已知三角形AOB的一个顶点为抛物线y²=2px(p为正常数)的顶点O,A,B两点都在抛线 2020-06-24 …
一个石头以初速度25米/秒,与水平方向夹角35度抛出.有可能以同样的初速度,但不同水平角抛出,却获 2020-06-24 …
两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”.为了便于记忆,同学们可仿 2020-07-03 …
在平面直角坐标系xOy中,把抛物线C1:y=x2-4沿x轴向右平移m(m>0)个单位长度,得抛物线 2020-07-26 …
表示抛物线的标准方程到底是什么(x-h)^2=4p(y-k)我在我学校里学的是这样的和中国的有什么 2020-08-02 …
物理平抛运动1、从10m高的楼顶,以45°的仰角抛出一个石子,落地点距抛出点的水平距离为10m,求该 2020-11-04 …
(2014•漳州质检)定义:若抛物线y=ax2+bx+c与x轴的两个交点和顶点构成直角三角形,则称这 2020-11-12 …
抛线物y=ax方与直线y=2x-3交于点a(m,-1),写出二次函数的表达式,并指出x取何值时yx的 2020-12-31 …
两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”。为了便于记忆,同学们可仿照 2021-01-17 …