早教吧作业答案频道 -->数学-->
在极坐标系中,曲线C的方程为ρ2=31+2cos2θ,点R(22,π4),以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(1)求曲线C的直角坐标方程及点R的直角
题目详情
在极坐标系中,曲线C的方程为ρ2=
,点R(2
,
),以极点为原点,极轴为x轴的正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)求曲线C的直角坐标方程及点R的直角坐标;
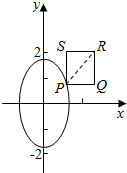
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
| 3 |
| 1+2cos2θ |
| 2 |
| π |
| 4 |
(1)求曲线C的直角坐标方程及点R的直角坐标;
(2)设P为曲线C上一动点,以PR为对角线的矩形PQRS的一边垂直于极轴,求矩形PQRS周长的最小值及此时点P的直角坐标.
▼优质解答
答案和解析
 (1)由x=ρcosθ,y=ρsinθ,
(1)由x=ρcosθ,y=ρsinθ,
∴曲线C的直角坐标方程为
+
=1,点R的直角坐标为(2,2),
(2)曲线C的参数方程为
(α为参数,α∈[0,2π)),
设P(cosα,
sinα),如图,依题意可得:
|PQ|=2-cosα,|QR|=2-
sinα,
∴矩形周长=2|PQ|+2|QR|=4-2cosα+4-2
sinα=8-4sin(α+
),
∴当α=
时,周长的最小值为4,此时,点P的坐标为(
,
).
 (1)由x=ρcosθ,y=ρsinθ,
(1)由x=ρcosθ,y=ρsinθ,∴曲线C的直角坐标方程为
| x2 |
| 1 |
| y2 |
| 3 |
(2)曲线C的参数方程为
|
设P(cosα,
| 3 |
|PQ|=2-cosα,|QR|=2-
| 3 |
∴矩形周长=2|PQ|+2|QR|=4-2cosα+4-2
| 3 |
| π |
| 6 |
∴当α=
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
看了 在极坐标系中,曲线C的方程为...的网友还看了以下:
1.小圆的直径等于大圆的半径,小圆的面积等于大圆面积的()①1/2②1/4③1/82.求一个半径为 2020-04-12 …
已知在Rt三角形ABC中,角ACB=90°,AC=6,BC=8,以点C为圆心,r为半径作圆.(1) 2020-04-27 …
1小时内请解答(简单)设外接球半径为R,内切球半径为r1)长方体,长a宽b高c则R=?2)正方体, 2020-05-14 …
在一首词曾有一句“坐地日行八万里”,这说明我们的地球在日夜不停地自转着,在地球上有一棵参天古树高3 2020-06-06 …
知道Y和R,求XR是半径可以用asin和acos一个圆,R是半径,圆上的某一点已知Y坐标,求这点对 2020-06-14 …
一个半径为R的半圆柱体沿水平向右以V匀速运动一个半径为R的半圆柱体沿水平方向向右以速度V0匀速运动 2020-06-27 …
1.半圆柱体重G,重心C到圆心O点的距离为α=4R/(3π),其中R为半圆柱半径,如半圆柱体与水平 2020-07-05 …
如图所示,直角坐标系Oxyz中,一半径为R的半圆和y轴的正半轴相切于M点,跟z轴负半轴相切,最低点 2020-07-31 …
一道数学题将半径为R的球加热,若球的半径增加△R,则球的体积增加△y约为()A4πR3△R/3B4π 2020-10-31 …
一题数学难题:小明想知道一个足球的半径小明想知道一个足球的半径,他用排水法测得体积为6280立方厘米 2020-11-26 …