早教吧作业答案频道 -->数学-->
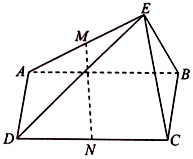
如图,在四棱锥E-ABCD中,平面EAB⊥平面ABCD,四边形ABCD为矩形,EA⊥EB,点M,N分别是AE,CD的中点.求证:(1)直线MN∥平面EBC;(2)直线EA⊥平面EBC.
题目详情
如图,在四棱锥E-ABCD中,平面EAB⊥平面ABCD,四边形ABCD为矩形,EA⊥EB,点M,N分别是AE,CD的中点.
求证:(1)直线MN∥平面EBC;
(2)直线EA⊥平面EBC.
求证:(1)直线MN∥平面EBC;
(2)直线EA⊥平面EBC.

▼优质解答
答案和解析
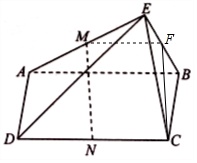 证明:(1)取BE中点F,连结CF,MF,
证明:(1)取BE中点F,连结CF,MF,
又M是AE的中点,所以MF=
AB,
又N是矩形ABCD边CD的中点,
所以NC=
AB,所以MF平行且等于NC,
所以四边形MNCF是平行四边形,…(4分)
所以MN∥CF,
又MN⊄平面EBC,CF⊂平面EBC,
所以MN∥平面EBC.…(7分)
(2)在矩形ABCD中,BC⊥AB,
又平面EAB⊥平面ABCD,平面ABCD∩平面EAB=AB,BC⊂平面ABCD,
所以BC⊥平面EAB,…(10分)
又EA⊂平面EAB,所以BC⊥EA,
又EA⊥EB,BC∩EB=B,EB,BC⊂平面EBC,
所以EA⊥平面EBC.…(14分)
 证明:(1)取BE中点F,连结CF,MF,
证明:(1)取BE中点F,连结CF,MF,又M是AE的中点,所以MF=
| 1 |
| 2 |
又N是矩形ABCD边CD的中点,
所以NC=
| 1 |
| 2 |
所以四边形MNCF是平行四边形,…(4分)
所以MN∥CF,
又MN⊄平面EBC,CF⊂平面EBC,
所以MN∥平面EBC.…(7分)
(2)在矩形ABCD中,BC⊥AB,
又平面EAB⊥平面ABCD,平面ABCD∩平面EAB=AB,BC⊂平面ABCD,
所以BC⊥平面EAB,…(10分)
又EA⊂平面EAB,所以BC⊥EA,
又EA⊥EB,BC∩EB=B,EB,BC⊂平面EBC,
所以EA⊥平面EBC.…(14分)
看了 如图,在四棱锥E-ABCD中...的网友还看了以下:
1、如图所示的一簇平等线为求知方向的匀强电场的电场线。沿与平行线成60°角的方向,把1μC负电荷以 2020-05-13 …
已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为() 2020-06-07 …
已知∠AOB=60°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为() 2020-06-07 …
已知∠AOB=160°,其角平分线为OM,∠BOC=20°,其角平分线为ON,则∠MON的大小为( 2020-06-07 …
如图,在△ABC中,AB=2,AC=BC=根号5.以AB所在的直线为x轴,AB的垂直平分线为y轴, 2020-06-27 …
已知P为椭圆上一点已知P为椭圆x^2/a^2+y^2/b^2=1(a>b>0)上一点,F1,F2为 2020-06-30 …
如图所示的一簇平行线为未知方向的匀强电场的电场线.沿与平行线成60°角的方向,把1μC负电荷以A点 2020-07-01 …
如图所示,一簇平行线为未知方向的匀强电场的电场线,沿与此平行线成60°角的方向,把1×10-3C的 2020-07-01 …
A、B为两等量异种电荷,图中水平虚线为A、B连线的中垂线,现将另两个等量异种的检验电荷a、b,如图 2020-07-17 …
高二解析几何,帮忙看下这道题目对不对在△ABC中,BC边上的高所在直线的方程是x-2y+1=0,∠ 2020-07-22 …