早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.(1)求证:PQ∥平面ABC1;(2)若AB=AA1,BC=3,AC1=3,BC1=13,求证:平面ABC1⊥平面AA1C1C.
题目详情
如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.
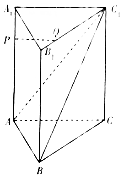
(1)求证:PQ∥平面ABC1;
(2)若AB=AA1,BC=3,AC1=3,BC1=
,求证:平面ABC1⊥平面AA1C1C.

(1)求证:PQ∥平面ABC1;
(2)若AB=AA1,BC=3,AC1=3,BC1=
| 13 |
▼优质解答
答案和解析
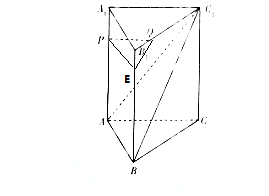 证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
∵在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q,
∴PE∥AB,QE∥BC1,
∵AB∩BC1=B,PE∩QE=E,AB、BC1⊂平面ABC1,
PE、QE⊂平面PQE,
∴平面ABC1∥平面PQE,
∵PQ⊂平面PQE,∴PQ∥平面ABC1.
(2)∵在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴AB⊥CC1,BC⊥CC1,
∵AB=AA1,BC=3,AC1=3,BC1=
,
∴AB=AA1=CC1=
=2,AC=
=
=
,
∴AB2+AC2=BC2,∴AB⊥AC,
又AC∩CC1=C,∴AB⊥平面AA1C1C,
∵AB⊂平面ABC1,∴平面ABC1⊥平面AA1C1C.
 证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,∵在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q,
∴PE∥AB,QE∥BC1,
∵AB∩BC1=B,PE∩QE=E,AB、BC1⊂平面ABC1,
PE、QE⊂平面PQE,
∴平面ABC1∥平面PQE,
∵PQ⊂平面PQE,∴PQ∥平面ABC1.
(2)∵在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴AB⊥CC1,BC⊥CC1,
∵AB=AA1,BC=3,AC1=3,BC1=
| 13 |
∴AB=AA1=CC1=
| 13-9 |
| AC12-CC12 |
| 9-4 |
| 5 |
∴AB2+AC2=BC2,∴AB⊥AC,
又AC∩CC1=C,∴AB⊥平面AA1C1C,
∵AB⊂平面ABC1,∴平面ABC1⊥平面AA1C1C.
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
若(p-q)的平方-(q-p)的立方=(q-p)的平方再乘以E则E是(1+p-q)求解答过程会有加 2020-05-20 …
如图,已知△ABC中,∠B=∠C,BD=5cm,BC=8cm.如果点P在线段BC上以3cm/s的速 2020-06-05 …
如图,A、C两点在直线L上,AC=6,D为射线CM上一点,CD=7,若在A、C两点之间栓一根橡皮筋 2020-06-11 …
已知集合P={x|x<-1或x>4},Q={x|a+1≤x≤2a-1}.若Q⊊P,求a的取值范围. 2020-06-12 …
一个高中集合和命题关系的问题命题p:-2≤x≤10,命题q:1-m≤x≤1+m,若q是P的必要而不 2020-06-14 …
设集合A={Xㄧ-1≤X≤a},P={yㄧy=x+1,x∈A},Q={y=x的平方,x∈A}(1) 2020-06-18 …
设集合P={x丨x的平方-4x-5<0},Q={x丨x-a<=0},(1)若PnQ=空集,求实数a 2020-08-01 …
(2014•宿迁模拟)已知公比为q(q≠1)的无穷等比数列{an}的首项a1=1.(1)若q=13 2020-08-02 …
已知函数f(x)=x+x+p,F(x)=f(f(x)).(1)若q=-2,试求F(x)的零点;求大神 2020-12-12 …
分别写出下列命题的逆命题、逆否命题,并判断它们的真假:(1)若q<1,则方程x2+2x+q=0有实根 2021-01-01 …