早教吧作业答案频道 -->数学-->
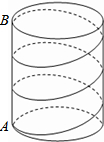
如图,圆柱底面圆的半径为2πcm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
题目详情
如图,圆柱底面圆的半径为
cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
| 2 |
| π |

▼优质解答
答案和解析
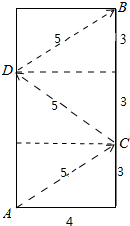 圆柱体的展开图如图所示,
圆柱体的展开图如图所示,
用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB,
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为
cm,
∴长方形的宽即是圆柱体的底面周长=2π×
=4cm,
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm,
根据勾股定理求得AC=CD=DB=5cm,
∴AC+CD+DB=15cm,
答:这根棉线的长度最短是15cm.
 圆柱体的展开图如图所示,
圆柱体的展开图如图所示,用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB,
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为
| 2 |
| π |
∴长方形的宽即是圆柱体的底面周长=2π×
| 2 |
| π |
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm,
根据勾股定理求得AC=CD=DB=5cm,
∴AC+CD+DB=15cm,
答:这根棉线的长度最短是15cm.
看了 如图,圆柱底面圆的半径为2π...的网友还看了以下:
椭圆方程问题.F1,F2为焦点,O为圆点,P为椭圆上任意一点.为什么向量PF1+向量PF2=2向量 2020-05-15 …
求解四点共圆奥数题作正三角形的外接圆,点P为劣弧AB上的一点,连接PC交AB于D,求证:1/PA+ 2020-05-17 …
圆锥底面半径为R,母线长3R,M是底面圆上一点,从点M拉一条绳子绕圆锥一圈,再回到点M,求M这根绳 2020-06-06 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
已知圆C:x^2+y^2+ax-4y+1=0(a属于R),过定点P(0,1)作斜率为1的直线交圆C 2020-06-09 …
描写关于坚韧的三个分论点从为什么?这个角度入手求快 2020-06-21 …
如图9所示,BC为半径等于2/5根号2m竖直放置的光滑细圆管,O为细圆管的圆心,在圆管的末端C连接 2020-07-11 …
以圆点O为圆心画个半圆这个弧线是不是算抛物线 2020-07-30 …
作正三角形的外接圆,点P为劣弧AB上的一点,连接PC交AB于D,求证:1/PA+1/PB=1/PD 2020-07-31 …
从圆柱体的表面点A开始,有一根绳子沿圆柱体表面绕圆的高为8cm,而底面圆周长为15cm,试求绳子的 2020-08-01 …