早教吧作业答案频道 -->数学-->
如图,ABC-A1B1C1是底面边长为2,高为32的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).(1)证明:PQ∥A1B1;(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投
题目详情
如图,ABC-A1B1C1是底面边长为2,高为
的正三棱柱,经过AB的截面与上
底面相交于PQ,设C1P=λC1A1(0<λ<1).
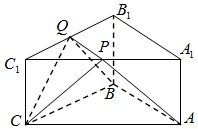
(1)证明:PQ∥A1B1;
(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四棱锥CABPQ表面积.
| ||
| 2 |
底面相交于PQ,设C1P=λC1A1(0<λ<1).

(1)证明:PQ∥A1B1;
(2)当CF⊥平面ABQP时,在图中作出点C在平面ABQP内的正投影F(说明作法及理由),并求四棱锥CABPQ表面积.
▼优质解答
答案和解析
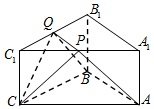 证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,又∵AB∥A1B1,∴PQ∥A1B1. (5分)
(Ⅱ)F点是PQ中点,理由如下:
当λ=
时,P,Q分别是A1C1,A1B1的中点,
连接CQ和CP,∵ABC-A1B1C1是正三棱柱,
∴CQ=CP,∴CF⊥QP,(6分)
取AB中点H,连接FH,CH,CH=
,
在等腰梯形ABQP中,FH=
,
连接CF,则CF=
,
∴CF2+FH2=CH2,∴CF⊥FH,
∵QP∩FH=H,∴CF⊥平面ABF,即CF⊥平面ABQP,(9分)
∴F点是C在平面ABQP内的正投影.
∴四棱锥CABPQ表面积:
S=S△CPQ+S△CPA+S△CQB+SPQBA+S△ABC=2
+
.(12分)
 证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,
证明:(I)∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,又∵AB∥A1B1,∴PQ∥A1B1. (5分)
(Ⅱ)F点是PQ中点,理由如下:
当λ=
| 1 |
| 2 |
连接CQ和CP,∵ABC-A1B1C1是正三棱柱,
∴CQ=CP,∴CF⊥QP,(6分)
取AB中点H,连接FH,CH,CH=
| 3 |
在等腰梯形ABQP中,FH=
| ||
| 2 |
连接CF,则CF=
| ||
| 2 |
∴CF2+FH2=CH2,∴CF⊥FH,
∵QP∩FH=H,∴CF⊥平面ABF,即CF⊥平面ABQP,(9分)
∴F点是C在平面ABQP内的正投影.
∴四棱锥CABPQ表面积:
S=S△CPQ+S△CPA+S△CQB+SPQBA+S△ABC=2
| 3 |
| 6 |
看了 如图,ABC-A1B1C1是...的网友还看了以下:
(2014•太原二模)三棱锥P-ABC,底面ABC为边长为23的正三角形,平面PBC⊥平面ABC, 2020-04-11 …
1.已知圆柱底面周长为6.28cm.高为6cm.求表面积和侧面积.2.已知圆柱底面直径为4cm.高 2020-05-14 …
在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC 2020-05-16 …
正四面体侧面与底面所成角为45度底面边长分别为3,4,5求侧面积.我是这样想的:底面积为6由面积射 2020-05-24 …
命题:①底面是正多边形,而且侧棱长与底面边长都相等的棱锥是正多面体;②正多面体的面不是三角形,就是 2020-06-27 …
圆锥面的压强计算公式一个圆锥上底直径d下底直径D长L(D>d\)在下底上面加一个F的力,求在圆锥表 2020-06-27 …
已知四棱锥P-ABCD中,平面PAD⊥平面ABCD,平面PCD⊥平面ABCD,E为PB上任意一点, 2020-07-31 …
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是根号3,D是AC的 2020-07-31 …
下列说法错误的是()A.用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 2020-07-31 …
棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱 2020-08-01 …