早教吧作业答案频道 -->数学-->
已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的直径,△ABC是边长为4的等边三角形,三棱锥P-ABC的体积为163,则该三棱锥的外接球的表面积.
题目详情
已知三棱锥P-ABC的四个顶点均在某球面上,PC为该球的直径,△ABC是边长为4的等边三角形,三棱锥P-ABC的体积为
,则该三棱锥的外接球的表面积___.
| 16 |
| 3 |
▼优质解答
答案和解析
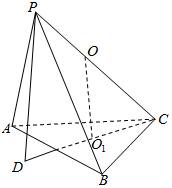 根据题意作出图形
根据题意作出图形
设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,
则OO1⊥平面ABC,延长CO1交球于点D,则PD⊥平面ABC.
∵CO1=
,
∴OO1=
,
∴高PD=2OO1=2
,
∵△ABC是边长为4正三角形,
∴S△ABC=
×42=4
∴V三棱锥P-ABC=
×4
×2
=
,
∴r2=
.
则球O的表面积为4πr2=
.
故答案为
.
 根据题意作出图形
根据题意作出图形设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,
则OO1⊥平面ABC,延长CO1交球于点D,则PD⊥平面ABC.
∵CO1=
4
| ||
| 3 |
∴OO1=
r2-
|
∴高PD=2OO1=2
r2-
|
∵△ABC是边长为4正三角形,
∴S△ABC=
| ||
| 4 |
| 3 |
∴V三棱锥P-ABC=
| 1 |
| 3 |
| 3 |
r2-
|
| 16 |
| 3 |
∴r2=
| 20 |
| 3 |
则球O的表面积为4πr2=
| 80π |
| 3 |
故答案为
| 80π |
| 3 |
看了 已知三棱锥P-ABC的四个顶...的网友还看了以下:
我们把任一四边形四边的中点依次连接成的四边形叫做中点四边形.(1)这个中点四边形有什么特征?请证明 2020-04-09 …
数控加工中心单边分中怎么理解啊,四边分中是两条边中点的交点好理解,单边就只分相邻的两条边,比如边长 2020-05-17 …
一个四边形,做它的内切圆,已知此圆过该四边形四边的中点,求这个四边形的形状 2020-05-24 …
我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形AB 2020-06-13 …
关于任意四边形分为两等面积部分的问题请问在任意一个四边形中,已经给定一条过顶点的好线(好线:在任意 2020-06-13 …
在给定的一个正n(n≥10)边形的n个顶点中任取k个点,使这k个点中存在4个点是某个四边形的顶点, 2020-06-13 …
各图形的中点四边形1.矩形的中点四边形2.菱形的中点四边形3.正方形的中点四边形4.四边形的中点四 2020-06-13 …
四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四 2020-07-30 …
我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形(1)任意四边形的中点四边形是什么形 2020-07-30 …
在四边形内找一点,使该点到各边距离都相等的图形是_____20,在四边形内找一点,使该点到各边距离 2020-07-30 …