早教吧作业答案频道 -->数学-->
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.(1)求证:AC⊥BF;(2)求证:BF⊥平面ACFD.
题目详情
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
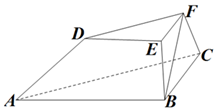
(1)求证:AC⊥BF;
(2)求证:BF⊥平面ACFD.

(1)求证:AC⊥BF;
(2)求证:BF⊥平面ACFD.
▼优质解答
答案和解析
(本小题满分12分)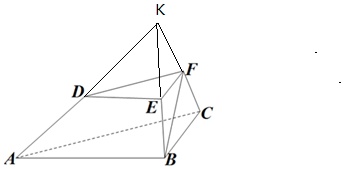
证明:(1)延长AD,BE,CF相交于一点K,如图所示,
因为平面BCEF⊥平面ABC,且AC⊥BC,
所以AC⊥平面BCK,
因为BF⊂平面BCK,所以BF⊥AC. …(6分)
(2)因为EF∥BC,BE=EF=FC=1,BC=2,
所以△BCK为等边三角形,且F为CK的中点,
则BF⊥CK,
又平面BCFE⊥平面ABC,∠ACB=90°,
所以AC⊥平面BCEF,
因为BF⊂平面BCEF,所以BF⊥AC,
又AC∩CK=C,
所以BF⊥平面ACFD…..(12分)

证明:(1)延长AD,BE,CF相交于一点K,如图所示,
因为平面BCEF⊥平面ABC,且AC⊥BC,
所以AC⊥平面BCK,
因为BF⊂平面BCK,所以BF⊥AC. …(6分)
(2)因为EF∥BC,BE=EF=FC=1,BC=2,
所以△BCK为等边三角形,且F为CK的中点,
则BF⊥CK,
又平面BCFE⊥平面ABC,∠ACB=90°,
所以AC⊥平面BCEF,
因为BF⊂平面BCEF,所以BF⊥AC,
又AC∩CK=C,
所以BF⊥平面ACFD…..(12分)
看了 如图,在三棱台ABC-DEF...的网友还看了以下:
在三角形ABC中,点D、E、F分别在AC,AB,BC边上且四边形CDEF是正方形,AC=3,BC= 2020-05-20 …
如图,在△ABC中,AB=AC=3,∠BAC=120°,以点A为圆心,1为半径作圆弧,分别交AB, 2020-06-14 …
(2013•河西区一模)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AC上(点 2020-07-30 …
已知定义在R上的奇函数f(x)满足f(x+1)=-f(x),且在[0,1]上递增,记a=f(12) 2020-08-01 …
(1)已知a>b>c,且a+b+c=0,用分析法求证:b2−ac<3a.(2)f(x)=13x+3 2020-08-01 …
一道数学中考题。在三角形ABC中,AB=AC=3,BC=4,E,F为AB,BC的任意一点,以EF为 2020-08-01 …
如图,将三角形纸片的一角折叠,使点B落在AC边上的F处,折痕为DE.已知AB=AC=3,BC=4, 2020-08-03 …
如图,已知△ABC中∠C=90°,BC=4,AC=3,点P是斜边AB上的一动点,作PE⊥BC于点E 2020-08-03 …
如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.(1)若 2020-11-02 …
如图,在RT△ABC中,∠C=90°,AC=3,BC=4,点E在直角边AC上,(点E不与A\C两点重 2020-11-07 …