早教吧作业答案频道 -->数学-->
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=2a,E,F分别是AD,AB的中点.(1)求证:平面EFB1D1∥平面BDC1;(2)求证:A1C⊥平面BDC1.
题目详情
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=
a,E,F分别是AD,AB的中点.
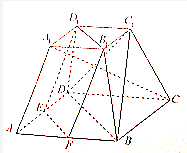
(1)求证:平面EFB1D1∥平面BDC1;
(2)求证:A1C⊥平面BDC1.
| 2 |

(1)求证:平面EFB1D1∥平面BDC1;
(2)求证:A1C⊥平面BDC1.
▼优质解答
答案和解析
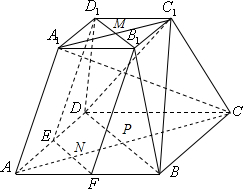 证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
由题意,BD∥B1D1,
因为BD⊄平面EFB1D1,B1D1⊂平面EFB1D1,所以BD∥平面EFB1D1…(3分)又因为A1B1=a,AB=2a,所以MC1=
A1C1=
a,
又因为E、F分别是AD、AB的中点,所以NP=
AC=
a,
所以MC1=NP,
又因为AC∥A1C1,所以MC1∥NP,
所以四边形MC1PN为平行四边形,
所以PC1∥MN;
因为PC1⊄平面EFB1D1,MN⊂平面EFB1D1,所以PC1∥平面EFB1D1,
因为PC1∩BD=P,所以平面EFB1D1∥平面BDC1…(6分)
(Ⅱ)连接A1P,因为A1C1∥PC,A1C1=PC=
a,
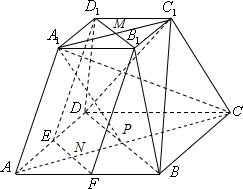
所以四边形A1C1CP为平行四边形,
因为CC1=AA1=PC=
a,所以四边形A1C1CP为菱形,
所以A1C⊥PC1…(9分)
因为MP⊥平面ABCD,MP⊂平面A1C1CA,
所以平面A1C1CA⊥平面ABCD;
因为BD⊥AC,所以BD⊥平面A1C1CA,
因为A1C⊂平面A1C1CA,所以BD⊥A1C,
因为PC1∩BD=P,所以A1C⊥平面BDC1.…(12分)
 证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,
证明:(Ⅰ)连接A1C1,AC,分别交B1D1,EF,BD于M,N,P,连接MN,C1P,由题意,BD∥B1D1,
因为BD⊄平面EFB1D1,B1D1⊂平面EFB1D1,所以BD∥平面EFB1D1…(3分)又因为A1B1=a,AB=2a,所以MC1=
| 1 |
| 2 |
| ||
| 2 |
又因为E、F分别是AD、AB的中点,所以NP=
| 1 |
| 4 |
| ||
| 2 |
所以MC1=NP,
又因为AC∥A1C1,所以MC1∥NP,
所以四边形MC1PN为平行四边形,
所以PC1∥MN;
因为PC1⊄平面EFB1D1,MN⊂平面EFB1D1,所以PC1∥平面EFB1D1,
因为PC1∩BD=P,所以平面EFB1D1∥平面BDC1…(6分)
(Ⅱ)连接A1P,因为A1C1∥PC,A1C1=PC=
| 2 |

所以四边形A1C1CP为平行四边形,
因为CC1=AA1=PC=
| 2 |
所以A1C⊥PC1…(9分)
因为MP⊥平面ABCD,MP⊂平面A1C1CA,
所以平面A1C1CA⊥平面ABCD;
因为BD⊥AC,所以BD⊥平面A1C1CA,
因为A1C⊂平面A1C1CA,所以BD⊥A1C,
因为PC1∩BD=P,所以A1C⊥平面BDC1.…(12分)
看了 如图,在正四棱台ABCD-A...的网友还看了以下:
设f(x)在[a,b]上可微,0小于a小于b.证明:在(a,b)内至少存在一点n.使得f(b)-f 2020-04-26 …
高数题目设f(x)在[a,b]上可导,又f'(x)+[f(x)]^2-∫(a到x)f(t)dt=0 2020-06-12 …
设函数f(x)在x=0处连续,且limh→0f(h2)h2=1,则()A.f(0)=0且f−′(0 2020-06-16 …
设f(x)在[a,b]上连续且可导,求证存在一点ξ∈(a,b),使f(b)-f(设f(x)在[a, 2020-07-13 …
已知f(x)在区间(﹣∞,+∞)上是减函数,a,b∈R,且a+b≤0,则下列正确的是?A.f(a) 2020-07-14 …
数学分析习题.设函数f(x)在[a,b]上三阶可导,证明:存在一点e∈(a,b)设函数f(x)在[ 2020-07-16 …
f(x)在[0,1]可导,f(x)满足f(0)=0,f(1)=1证明对任意的正数a,b,a/f'( 2020-07-16 …
(2014•达州一模)定义:如果函数y=f(x)在区间[a,b]上存在x1,x2(a<x1<x2< 2020-07-22 …
关于泰勒公示展开求证:已知f(x)在[a,b]存在二阶导数,f'(a)=f'(b)=0,则在存在c∈ 2020-11-23 …
已知f(x)在R上是增函已知f(x)在R上是增函数,a,b∈R,且a+b≤0,则有[]A、f(a)+ 2020-12-08 …