早教吧作业答案频道 -->数学-->
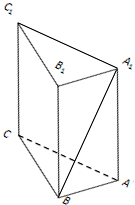
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=234,则球O的体积为.
题目详情
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
,则球O的体积为___.
| | 34 |

▼优质解答
答案和解析
因为三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,A1B1⊥B1C1,所以三棱柱的底面是直角三角形,侧棱与底面垂直,侧面A1ACC1,经过球的球心,球的直径是其对角线的长,
因为AA1=8,A1C1=2
,所以AC1=
=10
,所以球的半径为:5
,
所以球O的体积为
π×(5
)3=
π.
故答案为:
π.
因为AA1=8,A1C1=2
| 34 |
| 64+136 |
| 2 |
| 2 |
所以球O的体积为
| 4 |
| 3 |
| 2 |
1000
| ||
| 3 |
故答案为:
1000
| ||
| 3 |
看了 如图,已知三棱柱ABC-A1...的网友还看了以下:
以知a=1,b=2求1/ab+1/[a+1][b+1]+1/[a+2][b+2]+.+1/[a+2 2020-04-15 …
已知A,B,C的对数是a,b,c,且a+b+c=0,证明:A(1/b+1/c)×B(1/a+1/c 2020-05-16 …
已知函数f(x)=x^2+mx+n的图像过点(1,3),且f(-1+x)=(-1-x)对任意实数都 2020-06-08 …
2.证明:(1)a,b为不等的正整数,1/a、1/b的算术平均值为1/6==>a、b的算术;2.证 2020-06-13 …
已知二次函数y=ax平方的图像与直线y=2x-3交于点(1.b)(1)试求ab的值(2)求y=ax 2020-07-18 …
已知抛物线y=ax2(a≠0)与直线y=-2x+3交于点(-1,b)(1)求a,b的值(2)求抛物 2020-07-23 …
沿x轴正方向运动的A质点和B质点,其位置-时间图象(如图所示)分别为图中直线a和曲线b,已知B质点 2020-07-31 …
设曲线y=x的n+1次方(n属于N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,则x1乘以 2020-08-01 …
利用曲线积分与路径无关求积分∫L(e^y+x)dx+(xe^y–2y)dy,其中L为过三点O(0,0 2020-11-26 …
如图,平面直角坐标系中,A(-3,1)B(-1,4)1.求S△AOB2.直线AB交X轴于M点如图,平 2021-01-10 …