早教吧作业答案频道 -->数学-->
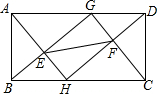
如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,(1)求证:四边形EHFG是矩形;(2)求EF的长.
题目详情
如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,
(1)求证:四边形EHFG是矩形;
(2)求EF的长.

(1)求证:四边形EHFG是矩形;
(2)求EF的长.
▼优质解答
答案和解析
(1)∵矩形ABCD中,AB=5,BE=3,AE=4,
∴AB2=AE2+BE2,∴∠GEH=∠AEB=90°,同理∠GFH=90°,
∵四边形ABCD是矩形,∴AB=CD,在△ABE与△CDF中,
,∴△ABE≌△CDF,∴∠DCG=∠BAH,∵∠BAH+∠GAE=∠BAH+∠GAH=90°,
∴∠BAH=∠GAH=∠DCG,
∴∠CGD+∠AGB=90°,
∴∠BGC=90°,
∴∠GEH=∠BGC=∠GFH=90°,
∴四边形EHFG是矩形;
(2)∵∠BAG=90°,AE⊥BG,
∴△ABE∽△AEG,
∴AE2=BE•GE,
∴EG=
=
,
同理GF=
=
=
,
∴EF=
=
.

∴AB2=AE2+BE2,∴∠GEH=∠AEB=90°,同理∠GFH=90°,
∵四边形ABCD是矩形,∴AB=CD,在△ABE与△CDF中,
|
∴∠BAH=∠GAH=∠DCG,
∴∠CGD+∠AGB=90°,
∴∠BGC=90°,
∴∠GEH=∠BGC=∠GFH=90°,
∴四边形EHFG是矩形;
(2)∵∠BAG=90°,AE⊥BG,
∴△ABE∽△AEG,
∴AE2=BE•GE,
∴EG=
| 4×4 |
| 3 |
| 16 |
| 3 |
同理GF=
| DF2 |
| CF |
| 32 |
| 4 |
| 9 |
| 4 |
∴EF=
| GE2+GF2 |
5
| ||
| 12 |
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
一块正方形的草地,边长为四米,在两个相对的角上各有一棵树,树上各拴了一只羊,拴羊的绳子长四米,问两 2020-04-07 …
(2014•义乌市三模)在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶 2020-05-14 …
在四边形ABCD中,延长CD至E,使得CE=BD,连接AE,∠ABD的角平分线与AE相交于点F.( 2020-06-13 …
协方差cov(X+20,Y+10)=cov(X,知道了COV(X+a,Y+b)=E[(X+a)(Y 2020-06-17 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点 2020-06-27 …
对数函数y=e^x-e^-x/e^x+e^-x转化为用含y的式子表示x的形式.谢咯,对数函数y=e 2020-07-15 …
对数函数y=e^x-e^-x/e^x+e^-x转化为用含y的式子表示x的形式.谢咯,对数函数y=e 2020-07-15 …
高数导数问题.设f(x)=(e^x-e^a)g(x)在x=a处可导,则函数g(x)应该满足条件是? 2020-07-20 …
读图,图中A点正午太阳高度角为0°.回答下列问题.(1)图中B、C、D、E四点的正午太阳高度角,由大 2021-01-23 …