早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=45,反比例函数y=kx的图象的一支经过AO的中点C,交AB于点D.(1)求反比例函数的解析式;(2)四边形OCDB的面积.
题目详情
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=
,反比例函数y=
的图象的一支经过AO的中点C,交AB于点D.
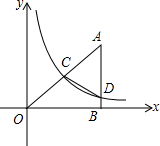
(1)求反比例函数的解析式;
(2)四边形OCDB的面积.
| 4 |
| 5 |
| k |
| x |

(1)求反比例函数的解析式;
(2)四边形OCDB的面积.
▼优质解答
答案和解析
(1)∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=
,
∴
=
,
∴OA=10,
由勾股定理得:AB=
=6,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),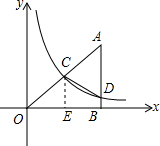
∵点C在反比例函数y=
的图象上,
∴k=12,
∴反比例函数解析式为:y=
;
(2)作CE⊥x轴于点E.则E的坐标是(4,0).
OE=BE=4,CE=3.
在y=
中,令x=8,解得y=
,则BD=
.
则S四边形OCDB=S△OCE+S梯形CEBD=
OE•CE+
(CE+BD)•BE=
×3×4+
(3+
)×4=6+9=15.
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=
| 4 |
| 5 |
∴
| OB |
| OA |
| 4 |
| 5 |
∴OA=10,
由勾股定理得:AB=
| OA2-OB2 |
∵点C是OA的中点,且在第一象限内,
∴C(4,3),

∵点C在反比例函数y=
| k |
| x |
∴k=12,
∴反比例函数解析式为:y=
| 12 |
| x |
(2)作CE⊥x轴于点E.则E的坐标是(4,0).
OE=BE=4,CE=3.
在y=
| 12 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
则S四边形OCDB=S△OCE+S梯形CEBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
如图,在半径为2的圆O中,点Q为优弧MN的中点,圆心角角MON=60°,在弧NQ上有一动点P,且点 2020-05-17 …
如图,在直棱柱ABO-A'B'O'中,OO'=4,OA=4,OB=3,∠AOB=90°,D是线段A 2020-06-27 …
在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB 2020-06-27 …
如下页图是一个隧道横截面,它的形状是以点o为圆心的圆的一部分,如果M是⊙o中的弦CD的中点,EM经 2020-07-05 …
如图,在半径是2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在NQ上有一动点P,且点P 2020-07-31 …
三角形ABC内接于圆O,连接AO并延长交圆O于点E,过点A做AD垂直BC于D(1)求证∠EAB=∠ 2020-07-31 …
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.(Ⅰ)将十字形的 2020-08-01 …
关于指数函数与图像的关系为什么指数函数中要想这个图像不过第二象限,a要大于1,不过第一象限,a大于 2020-08-02 …
高中立体几何4半径为r的圆O在平面@内,正三角形ABC内接于圆O,平面@外一点P在@内的射影是O点 2020-08-02 …
若两个二次函数的图象关于原点O中心对称,则称这个二次函数为“关于原点中心对称二次函数”.(1)请直接 2021-02-14 …