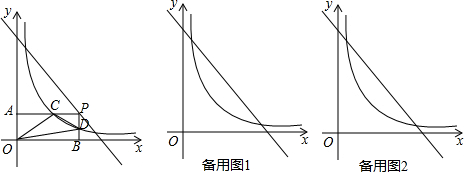
反比例函数y1=kx（x>0，k≠0）的图象进过点（1，3），P点是直线y2=-x+6上一个动点，如图所示，设P点的横坐标为m，且满足-m+6>3m，过P点分别作PB⊥x轴、PA⊥y轴，垂足分别为B、A，与双曲线

Question

反比例函数y₁=(k)/(x)（x>0，k≠0）的图象进过点（1，3），P点是直线y₂=-x+6上一个动点，如图所示，设P点的横坐标为m，且满足-m+6>(3)/(m)，过P点分别作PB⊥x轴、PA⊥y轴，垂足分别为B、A，与双曲线分别交于D、C两点，连接OC、OD、CD．
（1）求k的值并结合图象求出m的取值范围；
（2）在P点运动过程中，求线段OC最短时P点的坐标；
（3）将三角形OCD沿着CD翻折，点O的对应点为O′，得到四边形O′COD，问：四边形O′COD能否为菱形？若能，求出P点坐标；若不能，说明理由．

Answer 1

（1）∴反比例函数y₁=(k)/(x)（x>0，k≠0）的图象进过点（1，3），
∴把（1，3）代入y₁=(k)/(x)，解得k=3，
∵(3)/(m)=-m+6，
∴m=3±√(6)，
∴由图象得：3-√(6)<m<3+√(6)；

（2）∵线段OC最短时，
∴OC为∠AOB的平分线，
∵对于y₁=(3)/(x)，令x=y₁，
∴x=√(3)，即C（√(3)，√(3)），
∴把y=√(3)代入y=-x+6中，得：x=6-√(3)，即P（6-√(3)，√(3)）；

（3）四边形O′COD能为菱形，
∵当OC=OD时，四边形O′COD为菱形，
∴由对称性得到△AOC≌△BOD，即OA=OB，
∴此时P横纵坐标相等且在直线y=-x+6上，即x=-x+6，解得：x=3，即P（3，3）．