已知函数f（x）满足以下条件：①f（x）=2f（x-2）；②当x∈[-1，1]时，f（x）=|x|-1．（1）当x∈[-1，5]时，求函数y=f（x）+12的零点构成的集合；（2）当x∈[-7，0]∪（0，7）时，利用图象法判断

Question

已知函数f（x）满足以下条件：①f（x）=2f（x-2）；②当x∈[-1，1]时，f（x）=|x|-1．
（1）当x∈[-1，5]时，求函数y=f（x）+(1)/(2)的零点构成的集合；
（2）当x∈[-7，0]∪（0，7）时，利用图象法判断函数y=f（x）-log (1)/(3)|x|的零点个数．

Answer 1

（1）由y=f（x）+(1)/(2)=0得f（x）=-(1)/(2)，
①当x∈[-1，1]时，由f（x）=|x|-1=-(1)/(2)得|x|=(1)/(2)．
则x=(1)/(2)或-(1)/(2)，
②若1≤x≤3，则-1≤x-2≤1，
即f（x）=2f（x-2）=2（|x-2|-1）=2|x-2|-2，x∈[1，3]，
由f（x）=-(1)/(2)，得f（x）=2|x-2|-2=-(1)/(2)，即|x-2|=(3)/(4)，解得x=(5)/(4)或(11)/(4)．
③若3≤x≤5，则1≤x-2≤3，
即f（x）=2f（x-2）=2（2|x-4|-2）=4|x-4|-4，x∈[3，5]，
由f（x）=-(1)/(2)，得f（x）=4|x-4|-4=-(1)/(2)，即|x-4|=(7)/(8)，解得x=(25)/(8)或(39)/(8)．
即当x∈[-1，5]时，求函数y=f（x）+(1)/(2)的零点构成的集合为{(1)/(2)，-(1)/(2)，(5)/(4)，(11)/(4)，(25)/(8)，(39)/(8)}．
（2）由y=f（x）-log (1)/(3)|x|=0得f（x）=log (1)/(3)|x|，
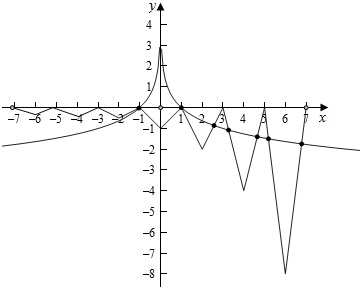
根据条件作出函数f（x）在[-7，0]∪（0，7）上的图象如图，作出y=log (1)/(3)|x|，
由图象知，两个函数在[-7，0]∪（0，7）上的交点个数为7个，
故函数y=f（x）-log (1)/(3)|x|的零点个数为7个．