早教吧作业答案频道 -->数学-->
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.(1)若AD=3,求△CAN的面积;(2)求证:AN=DM+2EF.
题目详情
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.
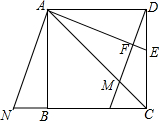
(1)若AD=3,求△CAN的面积;
(2)求证:AN=DM+2EF.

(1)若AD=3,求△CAN的面积;
(2)求证:AN=DM+2EF.
▼优质解答
答案和解析
(1) ∵四边形ABCD是正方形,
∴AD=AB=BC=CD=3,∠DAB=∠ABC=∠BCD=∠DC=90°,∠CAB=∠CAD=∠ACB=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5°,
∵AE⊥AN,
∴∠NAE=90°,∠NAC=90°-∠CAE=67.5°,∠N=180°-∠NAC-∠CN=67.5°,
∴∠N=∠NAC
∴CA=CN=
=
=3
,
∴S△ACN=
×CN×AB=
×3
×3=
.
(2)在FA上截取FH=FE,连接DH.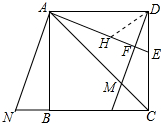
∵AE⊥DM,
∴DH=DE,
∴∠DHE=∠DEH=90°-∠DAE=67.5°,
∴∠MDC=∠HDF=90°-∠DEA=22.5°,
∴∠ADH=90°-∠HDE=45°,
∴∠ADH=∠MCD,∠DAH=∠MDC,
在△ADH和△DCM中,
,
∴△ADH≌△DCM,
∴AH=DM,
在△ABN和△ADE中,
,
∴△ABN≌△ADE,
∴AN=AE,
∴AN=AH+HE=DM+2EF.
∴AD=AB=BC=CD=3,∠DAB=∠ABC=∠BCD=∠DC=90°,∠CAB=∠CAD=∠ACB=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5°,
∵AE⊥AN,
∴∠NAE=90°,∠NAC=90°-∠CAE=67.5°,∠N=180°-∠NAC-∠CN=67.5°,
∴∠N=∠NAC
∴CA=CN=
| AB2+BC2 |
| 32+32 |
| 2 |
∴S△ACN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
9
| ||
| 2 |
(2)在FA上截取FH=FE,连接DH.

∵AE⊥DM,
∴DH=DE,
∴∠DHE=∠DEH=90°-∠DAE=67.5°,
∴∠MDC=∠HDF=90°-∠DEA=22.5°,
∴∠ADH=90°-∠HDE=45°,
∴∠ADH=∠MCD,∠DAH=∠MDC,
在△ADH和△DCM中,
|
∴△ADH≌△DCM,
∴AH=DM,
在△ABN和△ADE中,
|
∴△ABN≌△ADE,
∴AN=AE,
∴AN=AH+HE=DM+2EF.
看了 已知正方形ABCD如图所示,...的网友还看了以下:
已知a,b为正有理数,设m=b/a,n=(2a+b)/(a+b).求证:根号2的大小在m,n之间. 2020-04-06 …
M=b/a^x(modp)怎么算,b=6,a=7,x=6,p=17,问M多少? 2020-04-26 …
诺f(x)是在[a,b]上的正值可微函数,则有点m属于(a,b),使:In[f(b)/f(a)]= 2020-06-13 …
设f(x)在[a,b]上可导,f((a+b)/2)=0,记M=sup{f''(x)}证明∫f(x) 2020-06-17 …
m为偶数,则(a-b)^m·(b-a)^m+n(a≠b)的结果是A.相等B.互为相反数C.不相等D 2020-07-20 …
已知m,n是小于5的正整数,且(a-b)^m/(b-a)^n=a-b,求m,n的值写出具体过程,题 2020-07-20 …
我又问数学题来了.1.x=1-1/y,y=1-1/z,则用z表示x为?2.﹙2m/m+2-m/m- 2020-07-30 …
一道微积分的题目,急救设f(x)在[a,b]上连续,在(a,b)内二阶可导,且对x∈(a,b),| 2020-08-02 …
1.若(a^n*b^m*b)³=a^9*b^15,求2^m+n的值.2.计算;a^n-5(a^n+1 2020-11-01 …
关于X的方程a(x+m)^2+b=0的解是x1=-2,x2=1(a,m,b均为常数,a不等于0),则 2020-12-23 …