早教吧作业答案频道 -->数学-->
在△ABC中,点D在BC边上,且满足CA2=CD•CB(如图1)(1)求证:ADAB=ACBC;(2)如图2,以点A为圆心,AB为半径画弧交AC的延长线于点E,联结BE,延长AD交BE于点F,求证:EFBF=ADBD
题目详情
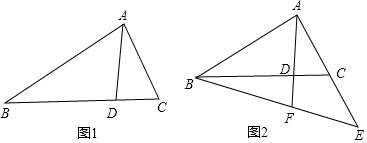
在△ABC中,点D在BC边上,且满足CA2=CD•CB(如图1)
(1)求证:
=
;
(2)如图2,以点A为圆心,AB为半径画弧交AC的延长线于点E,联结BE,延长AD交BE于点F,求证:
=
(1)求证:
| AD |
| AB |
| AC |
| BC |
(2)如图2,以点A为圆心,AB为半径画弧交AC的延长线于点E,联结BE,延长AD交BE于点F,求证:
| EF |
| BF |
| AD |
| BD |

▼优质解答
答案和解析
证明:(1)∵CA2=CD•CB,
∴CA:CD=CB:CA
∵∠C=∠C,
∴△CAB∽△CDA,
∴
=
;
(2)如图,过点B作BG∥AE,交AF的延长线于点G,
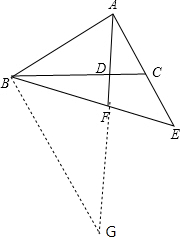
∵△ACD∽△BCA,
∴∠CAD=∠CBA,
∵BG∥AE,
∴∠G=∠CAD,
∴∠G=∠CBA,
又∠BAD=∠GAB,
∴△ABD∽△AGB,
∴
=
,即
=
,
∵BG∥AE,
∴
=
,
又∵AE=AB,
∴
=
,
∴
=
.
∴CA:CD=CB:CA
∵∠C=∠C,
∴△CAB∽△CDA,
∴
| AD |
| AB |
| AC |
| BC |
(2)如图,过点B作BG∥AE,交AF的延长线于点G,

∵△ACD∽△BCA,
∴∠CAD=∠CBA,
∵BG∥AE,
∴∠G=∠CAD,
∴∠G=∠CBA,
又∠BAD=∠GAB,
∴△ABD∽△AGB,
∴
| AD |
| AB |
| BD |
| GB |
| AB |
| GB |
| AD |
| BD |
∵BG∥AE,
∴
| EF |
| BF |
| AE |
| GB |
又∵AE=AB,
∴
| EF |
| BF |
| AB |
| GB |
∴
| EF |
| BF |
| AD |
| BD |
看了 在△ABC中,点D在BC边上...的网友还看了以下:
翻译文言文画蛇添足画蛇添足楚有祠者,赐其舍人卮酒.舍人相谓曰:"数人饮之不足,一人饮之有余.请画地 2020-05-13 …
求一几何证明题思路在矩形ABCD中,点E是对角线BD上一点,作角CEF=角CBD,过点C作CF垂直 2020-05-13 …
下图为1958年出现在我国的一幅宣传画,画上配的文字是:肥猪赛大象,就是鼻子短,全社杀一口,足够吃 2020-06-22 …
如图为1958年出现在我国的一幅宣传画,画上配的文字是:肥猪赛大象,就是鼻子短,全社杀一口,足够吃半 2020-11-04 …
下图为1958年出现在我国的一幅宣传画,画上配的文字是:肥猪赛大象,就是鼻子短,全社杀一口,足够吃半 2020-11-04 …
画平行线,并证明.我们在画垂线时需要标出垂足才能证明是垂线,哪平行线呢怎样证明? 2020-11-16 …
不足之处有一天,某城市繁华的街上,有个人在卖画。他卖的画上画的是一个小孩瞪着眼睛,张着嘴,正在数苹果 2020-11-20 …
孔子说:“夏礼吾能言之,杞不足征(证)也。殷礼吾能言之,宋不足征(证)也。文献不足故也。足,则吾能征 2020-12-09 …
如图为三位同学们所画的蝴蝶,下列评价正确的是()A.三图都描绘了昆虫具有头、胸、腹三部分;翅和足;身 2020-12-17 …
救急阿.证明题如图,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E 2020-12-19 …