如图，已知P为O外一点，连结OP交O于点A，且OA=2OP，求作直线PB，使PB与O相切．以下是甲、乙两同学的作业．甲：作OP的中垂线，交O于点B，则直线PB即为所求．乙：取OP的中点M，以M为圆心，

Question

如图，已知P为 O外一点，连结OP交 O于点A，且OA=2OP，求作直线PB，使PB与 O相切．以下是甲、乙两同学的作业．
甲：作OP的中垂线，交 O于点B，则直线PB即为所求．
乙：取OP的中点M，以M为圆心，OM长为半径画弧，交 O于点B，则直线PB即为所求．
对于两人的作业，下列说法正确的是（　　）

A. 两人都对

B. 两人都不对

C. 甲对，乙不对

D. 甲不对，乙对

Answer 1

如图1，OP的垂直平分线交OP于H，连结OB，设AP=x，则OA=2x，OB=2x，
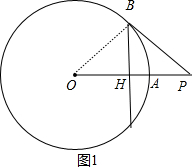
∵BH垂直平分OP，
∴BO=BP=2x，
∵OB²+BP²=（2x）²+（2x）²=4x²，
OP²=（3x）²=9x²，
∴△OBP不是直角三角形，
∴PB不是 O的切线；所以甲的说法错误；
如图2，连结OB，
∵M点为OP的中点，
∴OP为 M的直径，
∴∠OBP=90°，
∴OB⊥PB，
∴PB与 O相切；所以乙的说法正确．
故选D．