早教吧作业答案频道 -->数学-->
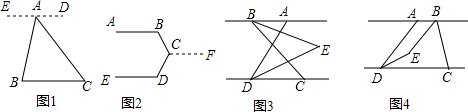
课题学习:平行线的“等角转化”功能.阅读理如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.(1)阅读并补充下面推理过程.过点A作ED∥BC,所以∠B=,∠C=.又因为
题目详情
课题学习:平行线的“等角转化”功能.
阅读理
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程.
过点A作ED∥BC,所以∠B=___,∠C=___.
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
解题反思:
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
提示:过点C作CF∥AB.
深化拓展:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
请从下面的A,B两题中任选一题解答,我选择___题.
A.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为___°.
B.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为___°.(用含n的代数式表示)
阅读理
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程.
过点A作ED∥BC,所以∠B=___,∠C=___.
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
解题反思:
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
提示:过点C作CF∥AB.
深化拓展:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
请从下面的A,B两题中任选一题解答,我选择___题.
A.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为___°.
B.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为___°.(用含n的代数式表示)

▼优质解答
答案和解析
 (1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
故答案为:∠EAD,∠DAE;
(2)过C作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
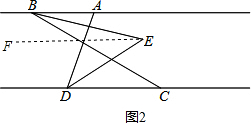
(3)A、如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=
∠ABC=30°,∠CDE=
∠ADC=35°,
∴∠BED=∠BEF+∠DEF=30°+35°=65°;
故答案为:65;
B、如图3,过点E作EF∥AB,
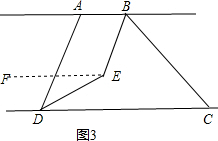 ∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∴∠ABE=
∠ABC=
n°,∠CDE=
∠ADC=35°
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°-
n°+35°=215°-
n°.
故答案为:215°-
n.
 (1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,故答案为:∠EAD,∠DAE;
(2)过C作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
(3)A、如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BED=∠BEF+∠DEF=30°+35°=65°;
故答案为:65;
B、如图3,过点E作EF∥AB,
 ∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-
| 1 |
| 2 |
∴∠BED=∠BEF+∠DEF=180°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:215°-
| 1 |
| 2 |
看了 课题学习:平行线的“等角转化...的网友还看了以下:
《列夫托尔斯泰》作者在课文前半部分极力描写托尔斯泰平庸甚至丑陋的外表,对塑造人物形象有什么作用?答 2020-05-14 …
过直线外一点,能作条已知直线的平行线,在同一平面内,能作条已知直线的平行线. 2020-07-14 …
高中必修4P119页第14题求答案如图所示,支座A受F1,F2两个力的作用,已知|F1|=40N, 2020-07-18 …
课堂上学生做实验用了五分之一小时,老师讲解用了十分之三小时,其余时间学生独立做作业.已知每堂课是三 2020-07-20 …
求一篇关于课外读物的英语作文或已课外读物为题的英语作文 2020-07-26 …
阅读短文,回答问题。寒假该读什么书三毛:我是个学生,平常课业压力甚重,在课余只能阅读一些翻译作品和中 2020-11-02 …
照样子,写句子。1.邓小平爷爷亲手栽种的柏树已经长大了。我的作业已经 ...照样子,写句子。 2020-11-26 …
怎么写在以前自己课前预习.课堂听课.课下作业.课后复习.课外阅读及练笔的状况:日记一篇(写在以前自己 2020-11-28 …
制作一张课桌需要1.2平方米的木板,20平方米的木板最多可制作几张这样的课桌? 2020-11-28 …
2013年6月11日,我国载人航天飞船“神舟十号”成功发射,在轨飞行15天,并首次开展中国航天员太空 2020-11-28 …