早教吧作业答案频道 -->数学-->
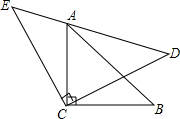
如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
题目详情
如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)

▼优质解答
答案和解析
证明:连结BD,
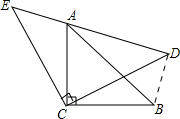
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-∠ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.

∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-∠ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
|
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.
看了 如图,在等腰直角三角形Rt△...的网友还看了以下:
一个圆如果直径减少了十厘米,那么半径就减少()厘米,如果半径增加了三厘米,那么直径就增加(一个圆如果 2020-03-30 …
一个圆,如果直径减少十厘米,那么半径就是减少()厘米,如果半径增加3厘米,那么直径就增加(一个圆, 2020-04-25 …
一个圆的直径是8cm,如果直径扩大到原来的2倍,周长增加多少厘米?如果直径增加7cm,则面积增加多 2020-06-04 …
关于金属热涨冷缩的问题例如:一截圆钢外直径240内直径120长210内孔加热后直径为120.4冷却 2020-06-16 …
如图甲所示,一物块在斜面上恰能以速度v0匀速下滑,斜面静止不动,若在物块上再施加如图乙所示的作用力 2020-06-27 …
如图,如果直线l上依次有三个点ABC,那么在直线L上共有多少条射线?多少条线段?再增加一个点,共增 2020-07-25 …
如图,如果直线L上依次有3个点A、B、C,那么(1)在直线L上共有多少射线?多少条线段?(2)在直 2020-07-25 …
比较级加er的单词有哪些直接加er列如longershorterolderyounger直接加er列 2020-10-31 …
不知道如何用公式表达:0+1+2+3+4+5+6+7+8一直加到n等等;且需要满足条件为:一起加的个 2020-11-20 …
如图,如果直线L上依次有3个点A、B、C,那么(1)在直线L上共有多少射线?多少条线段?(2)在直线 2020-12-05 …