早教吧作业答案频道 -->数学-->
已知y=ax2+bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:(1)4a+b=0;(2)c+9a>3b;(3)8a+7b+2c<0.正确结论有几个?
题目详情
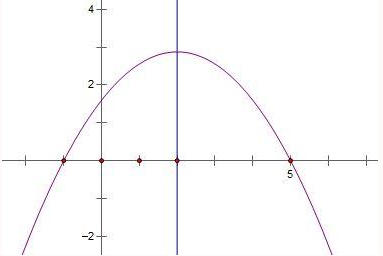 已知y=ax 2 +bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:
已知y=ax 2 +bx+c(a<0),图象过点(-1,0),对称轴为x=2,有下列结论:(1)4a+b=0;(2)c+9a>3b;(3)8a+7b+2c<0.
正确结论有几个?
▼优质解答
答案和解析
考点:
二次函数图象与系数的关系
专题:
分析:
(1)利用抛物线的对称轴即可判定;(2)把x=-3时代入即可判定;(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
(1)∵抛物线的对称轴为x=-b2a=2,∴b=-4a,即4a+b=0,所以①正确.(2)∵当x=-3时,y<0,∴9a-3b+c<0,即c+9a<3b.∴②错误.(3)∵抛物线与x的交点为(-1,0),∴a-b+c=0,∵b=-4a,a+4a+c=0,即c=-5a,∴8a+7b+2c=8a-28a-10a=-30a,∵a<0,∴8a+7b+2c>0. ∴③错误.所以正确的有1个.
点评:
本题主要考查了二次函数图象与系数关系,解题的关键是利用对称轴求出a,b的关系.
考点:
二次函数图象与系数的关系
专题:
分析:
(1)利用抛物线的对称轴即可判定;(2)把x=-3时代入即可判定;(3)由抛物线与x的交点为(-1,0),可得a-b+c=0,由b=-4a,可得c=-5a,化简8a+7b+2c=8a-28a-10a=-30a,由a<0,即可得8a+7b+2c>0.
(1)∵抛物线的对称轴为x=-b2a=2,∴b=-4a,即4a+b=0,所以①正确.(2)∵当x=-3时,y<0,∴9a-3b+c<0,即c+9a<3b.∴②错误.(3)∵抛物线与x的交点为(-1,0),∴a-b+c=0,∵b=-4a,a+4a+c=0,即c=-5a,∴8a+7b+2c=8a-28a-10a=-30a,∵a<0,∴8a+7b+2c>0. ∴③错误.所以正确的有1个.
点评:
本题主要考查了二次函数图象与系数关系,解题的关键是利用对称轴求出a,b的关系.
看了 已知y=ax2+bx+c(a...的网友还看了以下:
有7个杯子,杯口都朝上,每次翻3个,经过若干次能否将7个杯子杯口都朝下.可以用正负数表示, 2020-04-06 …
用when和Howlong开头的问句有哪些,不少于3个,要过去式 2020-05-13 …
生物学家发现一种胞子,每小时可分裂成3个,每个新胞子同原来的一样,一小时后它们中每个又都可以分裂成 2020-05-14 …
中国各个朝代君王的功过以及都城不用太复杂,每个君王例举1~3个功过就可以,并且标明其都城在里.例如 2020-05-16 …
一个平面内不在一直线上的3个点,过两点画一条直线,最多可以画几条直线? 2020-05-23 …
一个细胞一小时分裂三个,9小时可以把一个容器装满,多少时间使分裂的细胞装到容器的1/9.答案是七小 2020-05-23 …
有一个细胞分裂情况是这样的,一秒分裂成3个,再过一秒这三个又分别同时分裂成3个,依此类推,每个再同 2020-06-10 …
某种病毒繁殖非常快,每分钟繁殖到3个,经过4分钟,1个病毒会繁殖到多少个 2020-07-04 …
1.含有”反复琢磨”意思的词.(至少写3个,不过最好写多一点)2.照样子对对子.例:蓝天对白云黄金 2020-07-28 …
a、b是异面直线,a上有3个点,b上有3个点,过这6个点共能作平面()个A.2个B.9个C.6个D 2020-08-02 …