早教吧作业答案频道 -->数学-->
(1)问题发现:如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.填空:①四边形AFMG的形状是;
题目详情
(1)问题发现:
如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.
填空:①四边形AFMG的形状是___;
②△DFM和△MGE之间的关系是___.
(2)拓展探究:
如图2,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°,点F、M、G分别为AB、BC、AC边的中点,试判断△DFM和⊥MGE之间的关系,并加以说明.
(3)问题解决:
在(2)的条件下,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.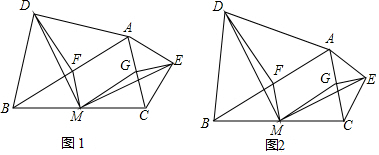
如图1,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.
填空:①四边形AFMG的形状是___;
②△DFM和△MGE之间的关系是___.
(2)拓展探究:
如图2,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°,点F、M、G分别为AB、BC、AC边的中点,试判断△DFM和⊥MGE之间的关系,并加以说明.
(3)问题解决:
在(2)的条件下,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.

▼优质解答
答案和解析
(1)①∵BF=AF,BM=MC,
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
故答案为:平行四边形;
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS);
故答案为:△DFM≌△MGE.
(2)△DFM∽△MGE,理由如下:
∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
AC=AG MG=
AB=AF.
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,
即∠DFM=∠MGE.
∵∠BAD+∠CAE=90°,∠CAE+∠AEG=90°,
∴∠BAD=∠AEG.
∴tan∠BAD=tan∠AEG.
∴
=
,即
=
,
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
(3)∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
=
=4.
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
=(
)2=(
)2=
.
∴S△MGE=32×
=18.
∴FM∥AC,同理MG∥AB,
∴四边形AFMG是平行四边形,
故答案为:平行四边形;
②∵∠BDA=90°,DF是AB边上的中线,
∴DF=AF.
∵四边形AFMG是平行四边形,
∴MG=AF,∠AFM=∠AGM.
∴DF=MG,∠BFM=∠MGC.
∵∠AEC=90°,EG是AC边上的中线,
∴GE=AG.
∵四边形AFMG是平行四边形,
∴AG=FM.
∴GE=FM.
∵DA=DB,F为AB的中点,
∴∠DFB=90°.
同理:∠EGC=90°.
∴∠DFB+∠BFM=∠EGC+∠MGC,即∠DFM=∠EGM.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS);
故答案为:△DFM≌△MGE.
(2)△DFM∽△MGE,理由如下:
∵△ADB和△ACE都是等腰三角形,且F、G为AB、AC的中点,
∴∠DFB=∠EGC=90°.
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BFM=∠BAC=∠MGC.
∴∠BFM+90°=∠MGC+90°,
即∠DFM=∠MGE.
∵∠BAD+∠CAE=90°,∠CAE+∠AEG=90°,
∴∠BAD=∠AEG.
∴tan∠BAD=tan∠AEG.
∴
| DF |
| AF |
| AG |
| GE |
| DF |
| MG |
| FM |
| GE |
又∵∠DFM=∠MGE,
∴△DFM∽△MGE.
(3)∵AD=5,AB=6,
∴AF=3,MG=3,MG=AF=3.
∴在Rt△ADF中,DF=
| AD2-AF2 |
| 52-32 |
∵由①知△DFM∽△MGE,且△DFM的面积为32,
∴
| S△MGE |
| S△DFM |
| MG |
| DF |
| 3 |
| 4 |
| 9 |
| 16 |
∴S△MGE=32×
| 9 |
| 16 |
看了 (1)问题发现:如图1,在△...的网友还看了以下:
要求简略过程1.在三角形ABC中,角A,B,C对边分别为a,b,c且满足(2a-c)cosB=bc 2020-05-15 …
已知△ABC中,a,b,c分别是角A.B.C所对的边,向量m→=(2sinB/2,√3/2).n→ 2020-05-22 …
如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O 2020-06-27 …
请教关于锐角三角函数题已知a.b.c分别是三角形ABC的三个内角角A.角B.角C的对边,当m大于0 2020-07-30 …
在锐角三角形中,角A,B,C的对边分别是a,b,c,角B=60,m=(sinA,1),n=(3,c 2020-07-30 …
1.已知a,b,c满足ab+a+b=bc+b+c=ca+c+a=3求(a+1)(b+1(c+1)的 2020-08-01 …
已知三角形ABC中,角A,角B,角C的对边分别是a、b、c(a大于b),关于x的方程x*2—2(a 2020-08-02 …
在梯行ABCD中,AD平行BC.角B等于40度.角C等于50度,E,M,F,N分别为AB,BC,CD 2020-11-01 …
三角形ABC中,角A,角B,角C的对边分别为a,b,c,抛物线y=x^2-2ax+b^2交x轴于两点 2020-11-12 …
在Rt三角形ABC中,AB=6cm,BC=8cm.角B=90度.M,N分别为AB,AC的中点,动点P 2020-11-20 …