如图所示，两同心圆圆心为O，半径分别为r和2r，在它们围成的环形区域内存在着磁感应强度为B、方向垂直纸面向里的匀强磁场，大量质量为m，电量为+q的带电粒子以不同的速率从P点沿各个

Question

如图所示，两同心圆圆心为O，半径分别为r和2r，在它们围成的环形区域内存在着磁感应强度为B、方向垂直纸面向里的匀强磁场，大量质量为m，电量为+q的带电粒子以不同的速率从P点沿各个方向射入磁场区域，不计粒子重力及其相互作用．

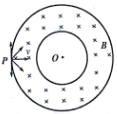
（1）若某带电粒子从P点沿PO方向射入磁场，恰好未能进人内部圆形区域，求该粒子在磁场中运动的时间；
（2）若有些带电粒子第一次穿过磁场后恰能经过O点，求这些粒子中最小的入射速率．

Answer 1

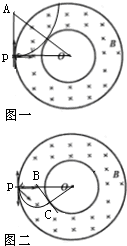（1）带电粒子从P点沿PO方向射入磁场，恰好未能进人内部圆形区域，说明运动轨迹正好与内圆相切，如图一；
设圆弧的半径为R₁圆心为A，连接OA、OP、AP，在直角三角形AOP中：OA²=OP²+AP²  
即：（R₁+r）²=R₁²+（2r）²
解得：R₁=1.5r
在直角三角形AOP中：tan∠A=(OP)/(AP)=(4)/(3)   所以∠A=53°
整个圆弧所对的圆心角为106°，带电粒子做圆周运动：
qvB=m(v2)/(R1)  
T=(2πR1)/(v)
解得：T=(2πm)/(qB)
粒子在磁场中运动的时间：t=(106°)/(360°)T=(53πm)/(90qB)
（2）欲求这些粒子中最小的入射速率，必须知道最小半径；粒子从P点经圆周运动沿半径通过圆心O，根据逆向运动，半径最小的圆周运动其圆弧与大圆内切，如图二；
设圆弧的半径为R₂圆心为B，PBO在一条直线上，连接OP、BC，在直角三角形OBC中：OB²=OC²+BC²   即（2r-R₂）²=r²+R₂²
解得：R₂=0.75r
带电粒子做圆周运动：qvB=m(v2)/(R2)
解得：v=(3qBr)/(4m)
答：（1）若某带电粒子从P点沿PO方向射入磁场，恰好未能进人内部圆形区域，求该粒子在磁场中运动的时间为(53πm)/(90qB)；
（2）若有些带电粒子第一次穿过磁场后恰能经过O点，求这些粒子中最小的入射速率为(3qBr)/(4m)．